#
Optik

#
Prisma
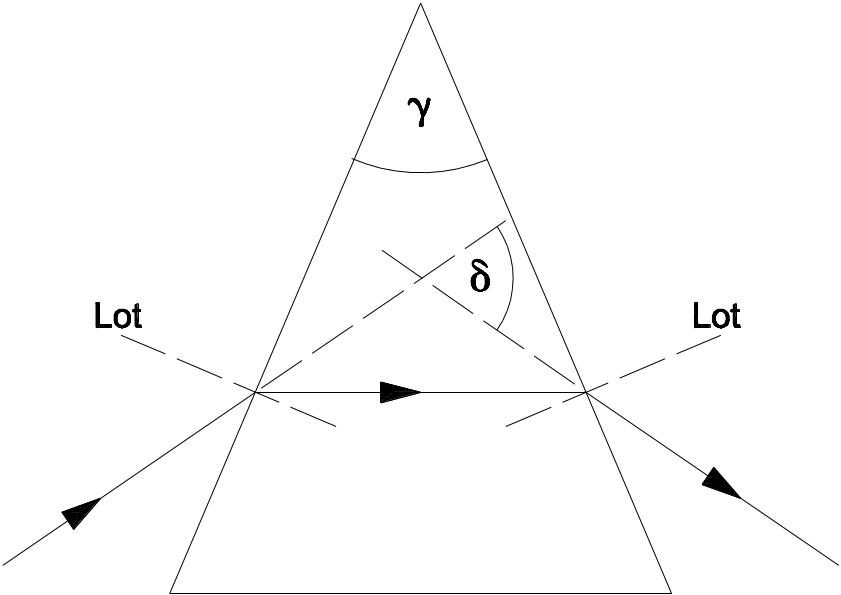
Ein Prisma besteht in der Regel aus Glas und muss mindestens zwei gegeneinander geneigte Flächen besitzen. Ein Prisma kann eine dreikantige (tetraederförmige) oder vierkantige (pyramidenförmige) Grundfläche besitzen. Durch die im Brechungsgesetz festgelegten Eigenschaften von Lichtstrahlen an den Grenzflächen von verschieden dicken Medien kommt es zu einer Brechung einfallender Lichtstrahlen an den Prismenkanten. Die beiden geneigten Prismenflächen bilden den Winkel , der auch als brechender Winkel bezeichnet wird. Trifft monochromatisches (einfarbiges) Licht auf eine Prismenkante auf, so dass es sich in dem Prisma parallel zur Grundfläche ausbreitet, gilt für die Ablenkung des Lichts folgende Beziehung:
\delta = \gamma \times (n - 1)
δ = gesamte Ablenkung des einfallenden parallelen Lichtbündels (gilt nur als gute Näherung für kleine )
γ = brechender Winkel des Prismas
n = Brechungsindex des Prismas
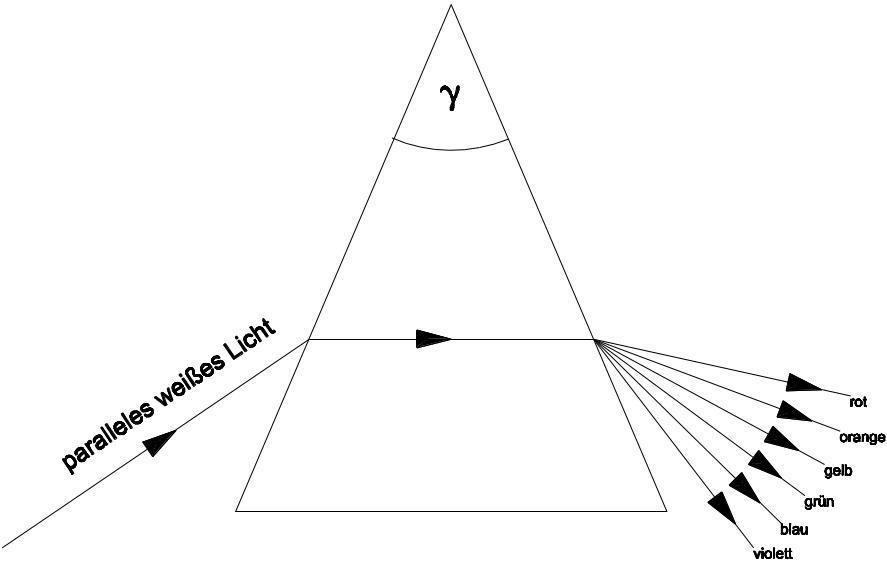
Wenn weißes Licht auf die Prismenkante auftrifft, bewirkt das Prisma die Dispersion des Lichtstrahls. Jede Farbe (Wellenlänge) des weißen Lichtstrahls wird wegen unterschiedlichen Brechungsindizes der einzelnen Wellenlängen verschieden stark gebrochen. Es findet eine Zerlegung des weißen Lichtstrahls in seine einzelnen Farbbestandteile (Spektralbestandteile) statt. Das entstehende Spektrum wird auch als Dispersionsspektrum bezeichnet.
#
Linsen
Linsen bestehen aus Glas oder anderen durchsichtigen Werkstoffen. Die weitest verbreiteten Linsen sind sphärische Linsen, bei denen die Linsenoberfläche einem Teil einer Kugeloberfläche entspricht. Die Lichtrichtung bei optischen Linsen ist jederzeit umkehrbar, so dass in den Brennpunkten z. B. punktförmige Lichtquellen positioniert werden können.
#
Sammellinsen (Konvexlinsen)
Sammellinsen sind in der Mitte stets dicker als am Rand. Es gibt drei verschiedene Formen der Sammellinsen.



Auftreffende Lichtstrahlen werden durch die Form der Sammellinse in einem Punkt gesammelt, dem sog. Brennpunkt F. Die Brennweite f bezeichnet den Abstand des Brennpunktes von der Linsenmitte. Der Brennpunkt ist definiert als Punkt einer dünnen Sammellinse, in dem parallel zur optischen Achse einfallende Lichtstrahlen vereinigt werden.
Wegen der chromatischen und sphärischen Abberation entstehen jedoch Abbildungsfehler, die in optischen Systemen durch den Einsatz entsprechender Linsensysteme korrigiert werden können.
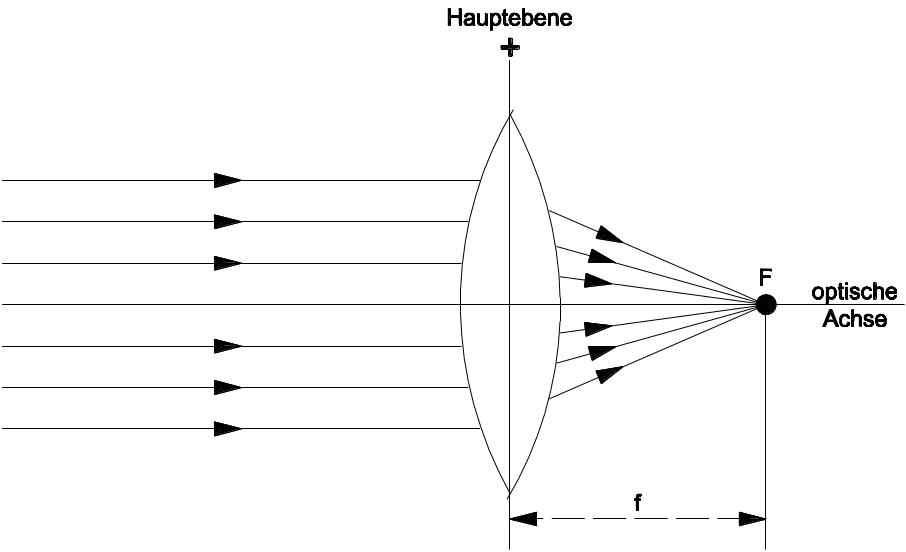
Die Lichtrichtung des einfallenden Lichts ist jederzeit umkehrbar, so dass z. B. für Scheinwerfersysteme in den Brennpunkten punktförmige Lichtquellen positioniert werden können.
Bilder der Sammellinse (f > 0):
reell = direkte Projektion auf Oberfläche möglich; virtuell = Bildweite liegt auf der Gegenstandsseite, Projektion nur mit einer weiteren Linse möglich
#
Zerstreuungslinsen (Konkavlinsen)
Zerstreuungslinsen bewirken, dass einfallende Lichtstrahlen die Linse divergierend (auseinanderstrebend) verlassen. Um diesen Effekt zu erzielen, muss die Linsenmitte einer Zerstreuungslinse dünner sein als der Linsenrand. Es gibt drei Arten von Zerstreuungslinsen.
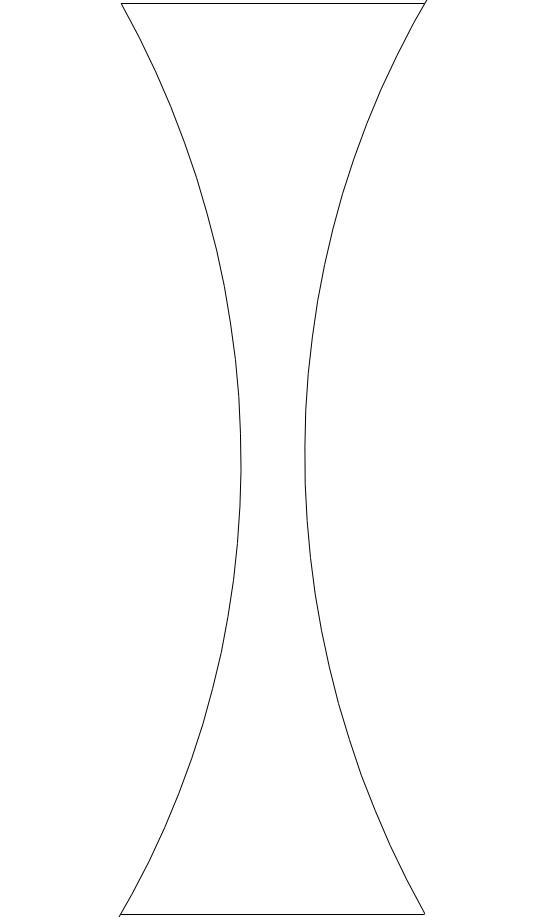
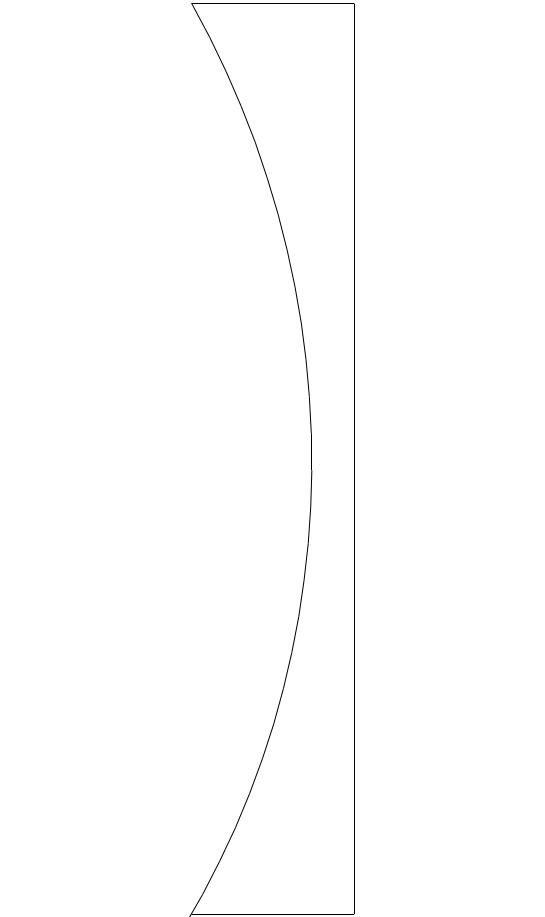
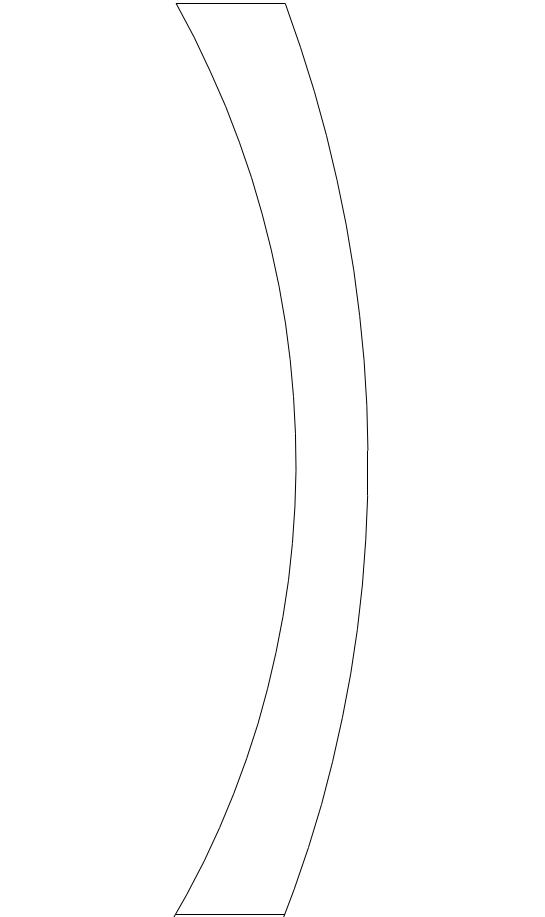
Zerstreuungslinsen besitzen wie Sammellinsen einen Brennpunkt FZ, in dem sich die rückwärtigen Verlängerungen von parallel zur optischen Achse einfallenden Lichtstrahlen vereinigen. Der Brennpunkt einer Zerstreuungslinse ist „virtuell“, da sich die parallel einfallenden Strahlen dort nicht tatsächlich treffen, sondern in der Verlängerung des Brennpunktes auseinanderstreben (siehe Abbildung).
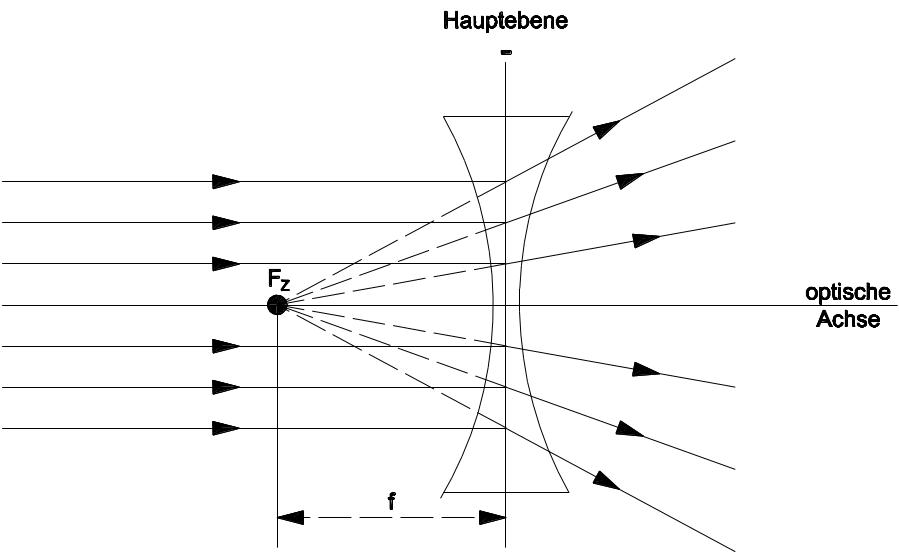
Liegt im Brennpunkt FZ einer Zerstreuungslinse eine punktförmige Lichtquelle, verlassen die Lichtstrahlen die Zerstreuungslinse parallel. Wegen des virtuellen Brennpunktes wird die Brennweite f (Abstand des Linsenmittelpunkts vom Brennpunkt) bei einer Zerstreuungslinse negativ gerechnet.
Auch hier entstehen wegen der chromatischen und sphärischen Abberation Abbildungsfehler, die in optischen Systemen durch den Einsatz entsprechender Linsensysteme korrigiert werden können.
Bilder der Zerstreuungslinse (f < 0):
virtuell = Bildweite liegt auf der Gegenstandsseite, Projektion nur mit einer weiteren Linse möglich
#
13.2.3 Fresnellinsen (Stufenlinsen)
Sammellinsen werden immer dann verwendet, wenn Lichtstrahlen möglichst parallel aus einem Linsensystem austreten sollen. Sammellinsen mit großen Durchmessern und kurzen Brennweiten sind jedoch sehr dick, haben ein großes Gewicht und sind bruchanfällig bei ungleichmäßiger Erwärmung der Linse. Zur Beseitigung dieser Nachteile entwickelte der französische Ingenieur und Physiker Jean Fresnel die nach ihm benannte Fresnel- oder Stufenlinse. Bei der Stufenlinse werden die Lichtstrahlen an einzelnen, sägezahnförmig angeordneten Ringen gebrochen. Da eine Brechung der Lichtstrahlen nur an den Grenzflächen der Linse stattfindet, kann die Oberfläche einer plan-konvexen Linse in mehrere, ineinander versetzte konzentrische Ringe aufgeteilt werden. Die Dicke der Linse wird wesentlich verkleinert bei gleichzeitiger Verminderung der Wärmeabsorption. Ein Aufrauen der Glasoberfläche vermindert eine Projektion der einzelnen Stufenringe.
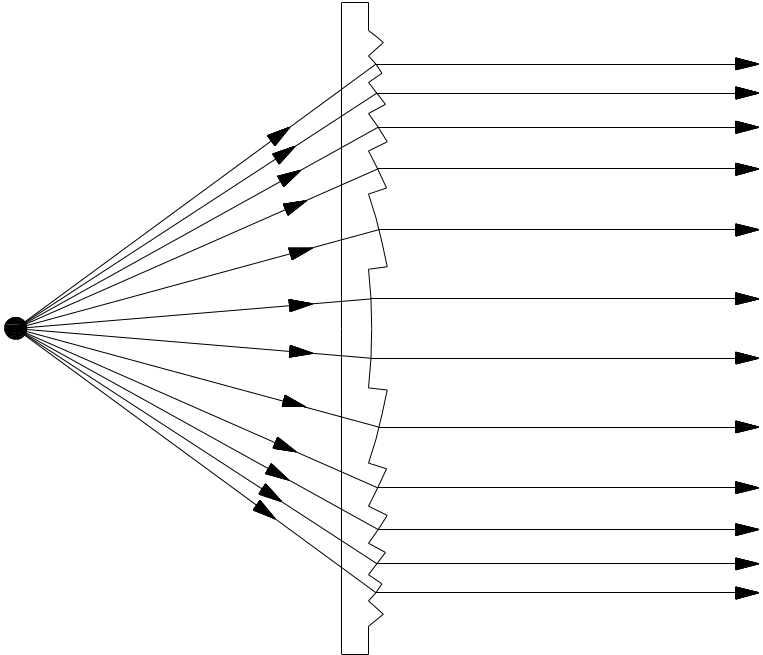
#
Linsengesetze
Die Abbildung eines Gegenstandes mit Hilfe einer Linse lässt sich über die Linsengesetze berechnen. Beim Durchlaufen einer Linse werden Lichtstrahlen zweimal gebrochen (jeweils an den Grenzen der Linse, siehe Brechungsgesetz). Zur Vereinfachung ersetzt man die Brechung an beiden Linsenoberflächen in Zeichnungen und Rechnungen durch die Brechung an zwei Hauptebenen. Bei dünnen Linsen, deren Dicke gegenüber den Krümmungsradien der Kugelflächen klein ist, fallen die Hauptebenen praktisch zusammen und liegen in der Mittelebene der Linse. Bei dünnen Linsen sind alle Abstände auf die Mittelebene bezogen.
#
Abbildungsgleichung
\frac{1}{f} = \frac{1}{b} + \frac{1}{g}f = Brennweite der Linse
g = Gegenstandsweite (Abstand des abzubildenden Gegenstands von der Linsenmitte)
b = Bildweite (Abstand des von der Linse erzeugten Bildes von der Linsenmitte)
Bei Zerstreuungslinsen ist die Brennweite f und die Bildweite b negativ!
Diese Gleichung gilt jedoch nur für unendlich dünne Linsen, die es in der Praxis jedoch nicht gibt. In guter Näherung gilt diese Gleichung für dünne Linsen unter der Voraussetzung, dass die Linsendicke klein ist gegenüber der Linsenlänge.
\beta = \frac{B}{G} + \frac{b}{g}β = Abbildungsmaßstab
(V > 0 ⇒ Bild ist aufrecht)
(V < 0 ⇒ Bild ist umgekehrt)
B = Bildgröße
G = Gegenstandsgröße
g = Gegenstandsweite (Abstand des abzubildenden Gegenstands von der Linsenmitte)
b = Bildweite (Abstand des von der Linse erzeugten Bildes von der Linsenmitte)
Bei Zerstreuungslinsen ist die Bildweite b negativ!
#
Linsen mit verschiedenen Krümmungsradien
\frac{1}{f} = (\frac{n}{n_M} - 1) \times (\frac{1}{r_1} - \frac{1}{r_2})f = Brennweite der Linse
n = Brechzahl des Linsenmaterials
nM = Brechzahl des umgebenden Mediums (Luft ≈ 1)
r1 = Radius der Lichteinfallseite (bei Sammellinse positiv, bei Zerstreuungslinse negativ)
r2 = Radius der Lichtausfallseite (bei Sammellinse neagtiv, bei Zerstreuungslinse positiv)
Krümmungsradien von nach außen gewölbten Linsen (Sammellinsen) sind immer positiv, Krümmungsradien von nach innen gewölbten Linsen (Zerstreuungslinsen) immer negativ. Die Formel gilt nur für dünne Linsen, deren Dicke klein ist gegenüber deren Länge.
#
Systeme dünner Linsen
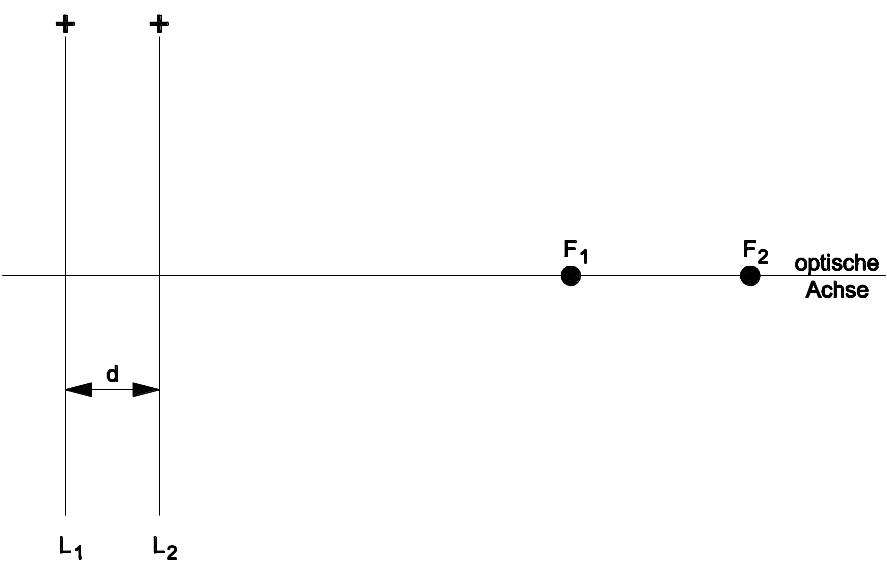
Systeme dünner Linsen wirken wie eine Linse, wenn der Abstand d der Linsen klein gegenüber der Linsenbrennweite f1 und f2 ist. Die Gesamtbrennweite ergibt sich aus der Kombination der Einzelbrennweiten.
\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2} - \frac{d}{f_1 \times f_2}f = Gesamtbrennweite der Linse
f1 = Brennweite der ersten Linse
f2 = Brennweite der zweiten Linse
d = Abstand beider Linsen
Bei Zerstreuungslinsen ist die Brennweite f negativ!
#
Dicke Linsen
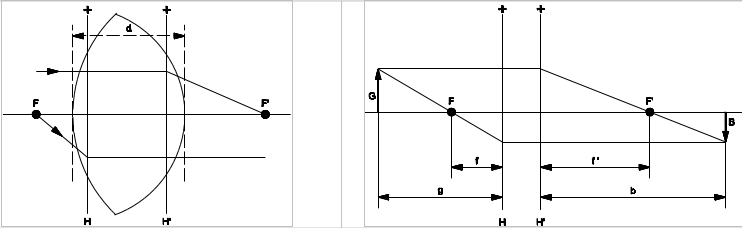
Bei dicken Linsen gelten die Abbildungsgesetze nur, wenn die Linse in zwei Hauptebenen aufgeteilt wird. Der Brennpunktstrahl wird an der ersten Hauptebene H gebrochen, der Parallelstrahl wird an der zweiten Hauptebene H’ gebrochen. Die Abstände f, f’, g und b beziehen sich stets auf die entsprechende Hauptebene.
\frac{1}{f} = (n-1)(\frac{1}{r_1} + \frac{1}{r_2}) - \frac{d(n-1)^2}{n \times r_1 \times r_2}f = Brennweite der Linse
n = Brechzahl des Linsenmaterials
r1 = Krümmungsradius der stärker gekrümmten Linsenfläche
r2 = Krümmungsradius der schwächer gekrümmten Linsenfläche
d = Abstand der beiden Linsenscheitel
#
Systeme dicker Linsen
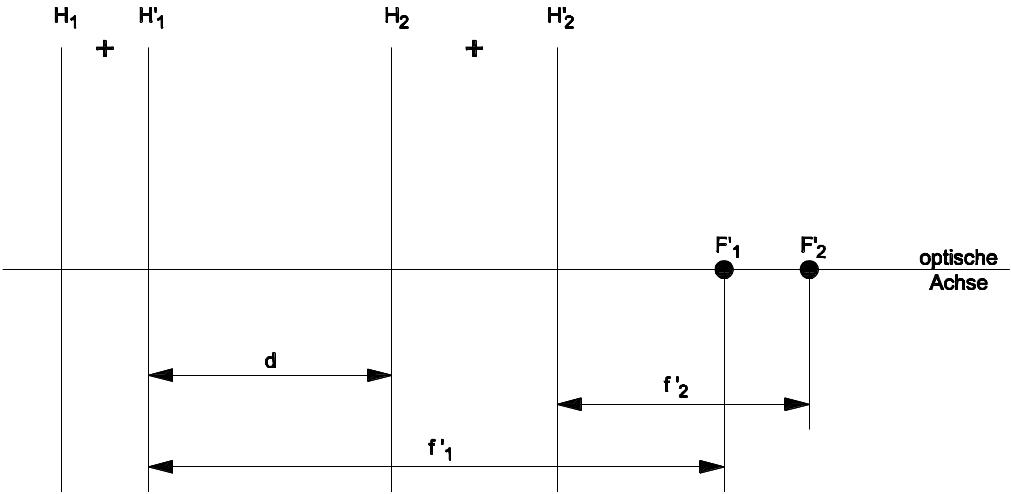
Bei Systemen dicker Linsen ergibt sich die Brennweite ebenfalls nach der Formel nach Abschnitt 13.3.4. Anstelle des Abstandes beider Linsen ist jedoch für d der Abstand der beiden einander zugekehrten Hauptebenen einzusetzen.
#
Der Strahlengang durch eine Linse lässt sich zeichnerisch ermitteln. Dabei werden für die Konstruktion drei charakteristische Strahlen verwendet:
- Mittelpunktstrahl, der ungebrochen durch den Mittelpunkt der Linse hindurchgeht
- Brennpunktstrahl, der durch den Brennpunkt der Linse geht und die Linse parallel zur optischen Achse verlässt
- Parallelstrahl, der nach Verlassen der Linse durch den Brennpunkt hindurchgeht
Bei der Zerstreuungslinse wird der Brennpunktstrahl zum Parallelstrahl und umgekehrt.
#
Projektionslinse
Wird ein abzubildender Gegenstand innerhalb des Bereichs zwischen einfacher (F) und doppelter (2F) Brennweite einer Sammellinse positioniert, so wird der Gegenstand auf der anderen Seite der Linse auf einem Schirm scharf abgebildet. Die Abbildung ist dabei umgekehrt, vergrößert und reell. Reell bedeutet, dass man die Abbildung ohne weitere Hilfsmittel (wie zusätzliche Linsen) auf einem Schirm auffangen kann. Projektionslinsen werden zum Beispiel in Diaprojektoren eingesetzt.
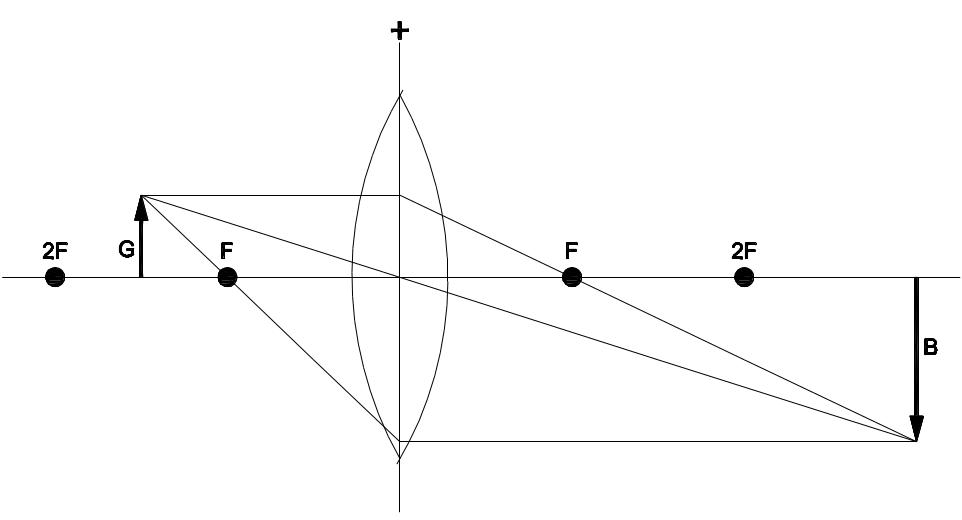
Eigenschaften der Projektionslinse:
#
Fotografische Linse
Im Gegensatz zu Projektionslinsen verkleinern fotografische Linsen die Abbildung eines Gegenstands. Dabei muss sich der abzubildende Gegenstand weit außerhalb der zweifachen Brennweite (2F) einer Sammellinse befinden. Die entstehende Abbildung auf der anderen Seite der Linse ist verkleinert, umgekehrt und reell. In jedem Fotoapparat befinden sich derartig wirkende Linsen, die als Optik oder Objektiv bezeichnet werden. Zum Ausgleich von optischen Fehlern eines Objektivs werden mehrere Linsen eingesetzt. Sammellinsen wirken als fotografische Linsen, wenn Gegenstände bei einer Objektivbrennweite von 50 mm weiter als 100 mm vom Objektiv entfernt sind. Der Strahlengang lässt sich wie bei der Projektionslinse zeichnerisch ermitteln.
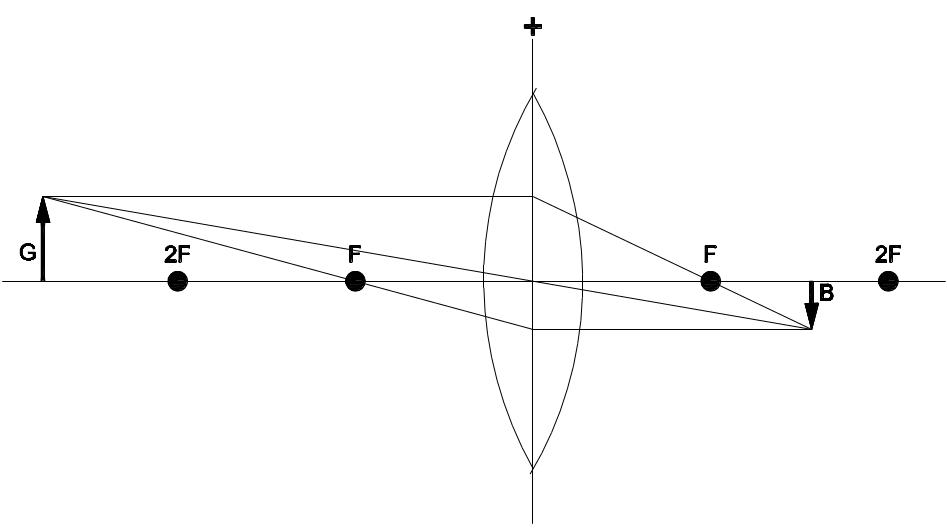
Eigenschaften der fotografischen Linse:
#
Lupe
Wird ein abzubildender Gegenstand bei einer Sammellinse zwischen Linse und einfacher Brennweite (F) positioniert, so entsteht kein reelles Bild, da die Strahlen hinter der Linse divergieren. Es lässt sich auf einem Schirm kein Bild auffangen. Mit Hilfe einer weiteren Linse wie der Augenlinse kann jedoch ein reelles Bild erzeugt werden. Die Abbildung erscheint dabei den Augen und dem Gehirn in der rückwärtigen Verlängerung der einfallenden Strahlen. Die Abbildung wird deshalb als virtuell bezeichnet. Eine Lupe erzeugt ein aufrechtes, virtuelles und vergrößertes Bild.
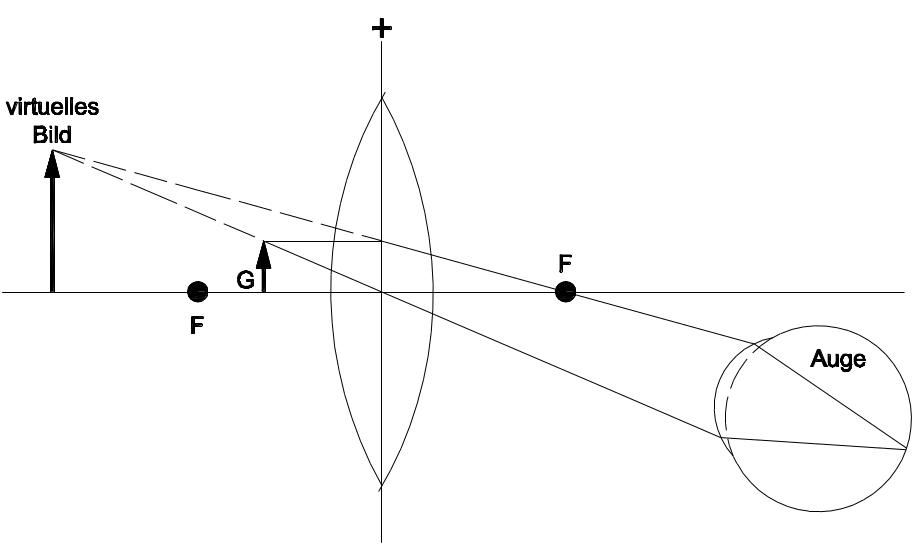
Eigenschaften der fotografischen Linse:
#
Brechkraft, Dioptrie
In der Optik, gerade in der medizinischen Optik, gibt man bei Linsen oft nicht die Brennweite F an, sondern ihre Brechkraft B in Dioptrie (dpt).
D = \frac{1}{f}D_{GES} = D_1 + D_2 + D_3 + ..... + D_ND = Brechkraft der Linse mit der Einheit Dioptrien [dpt in Meter]
f = Brennweite der Linse
DGES = gesamte Brechkraft eines Linsensystems (im Idealfall)
Das Rechnen mit Brechkräften anstelle von Brennweiten hat den Vorteil, dass sich die Brechkräfte mehrerer Linsen einfach addieren lassen. Dabei müssen jedoch im Idealfall die Abstände der Linsen zueinander so klein sein, dass sie vernachlässigt werden können.
#
Ebener Spiegel
Ein ebener Spiegel besteht aus einer glatten Oberfläche, an der einfallende Parallelstrahlen auch nach der Reflektion parallel sind. Ebene Spiegel dienen zur Bilderzeugung, bei der virtuelle Bilder entstehen, die symmetrisch mit dem Ursprungsgegenstand zum Spiegel liegen. Die aus dem Spiegel reflektierten Strahlen scheinen in einem Punkt hinter dem Spiegel zu entspringen.
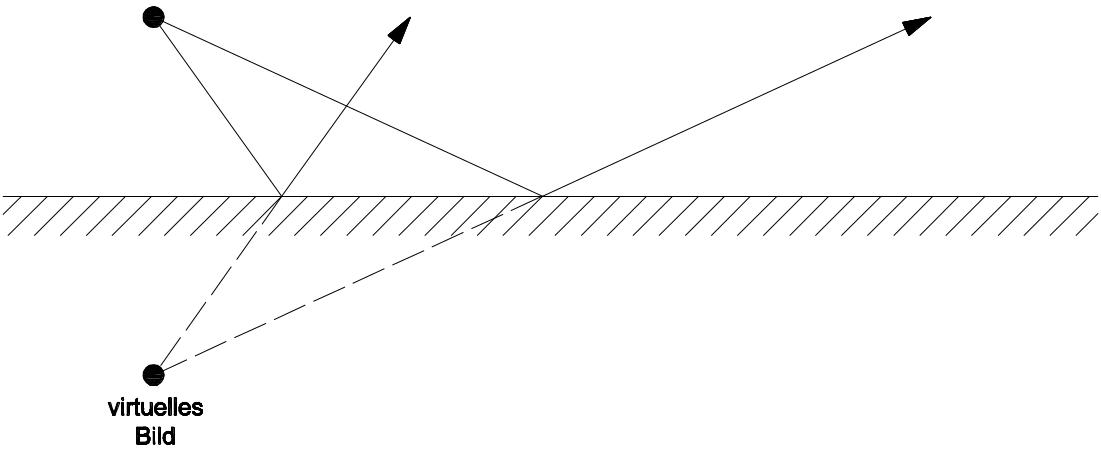
#
Hohlspiegel (Konkavspiegel)
Das Reflektionsgesetz lässt sich auch für gekrümmte Spiegelflächen anwenden. Die Flächennormale (Senkrechte zur Spiegelebene, Lot) hat jedoch für jeden Punkt der Spiegeloberfläche eine andere Richtung.
Viele der verwendeten Spiegel bestehen aus Aluminium und sind je nach Anwendung glänzend poliert oder matt angeraut. Für hohe Präzisionsansprüche werden Glassilberspiegel verwendet. Bei sog. Kaltlichtspiegeln ist auf der Spiegeloberfläche eine dichroitische Schicht aufgebracht. Diese reflektiert nur Wellenlängen des sichtbaren Lichts bei gleichzeitiger Ausspiegelung der Infrarotstrahlung (Wärme).
#
Zeichnerische Lösung des Strahlengangs
Die Reflektion eines Hohlspiegels lässt sich auch zeichnerisch ermitteln. Dabei werden wie bei den Linsensystemen die drei charakteristischen Strahlen verwendet:
- Mittelpunktstrahl, der in sich selber reflektiert wird
- Brennpunktstrahl, der durch den Brennpunkt des Hohlspiegels geht und nach der Reflektion parallel zur optischen Achse liegt
- Parallelstrahl, der nach der Reflektion durch den Brennpunkt des Hohlspiegels geht
#
Sphärische Spiegel
Sphärische Spiegel sind Teile einer Kugelfläche. Der Brennpunkt F mit der Brennweite f halbiert die Strecke zwischen Mittelpunkt und Scheitelpunkt der Kugelfläche.
f = \frac{r}{2}\frac{1}{f} = \frac{1}{b} + \frac{1}{g}\frac{G}{B} = \frac{g}{b} = \frac{1}{\beta}f = Brennweite der Linse
r = Radius der Kugelfläche
G = Gegenstandsgröße
B = Bildgröße
g = Gegenstandsweite (Abstand des abzubildenden Gegenstands vom Spiegel)
b = Bildweite (Abstand des von der Linse erzeugten Bildes)
β = Abbildungsmaßstab
Parallel zur optischen Achse einfallende Lichtstrahlen werden von der Kugelfläche im Brennpunkt gesammelt. Wegen der Umkehrbarkeit des Strahlengangs werden die Lichtstrahlen einer im Brennpunkt des Spiegels liegenden Lichtquelle nach der Reflektion annähernd parallel.
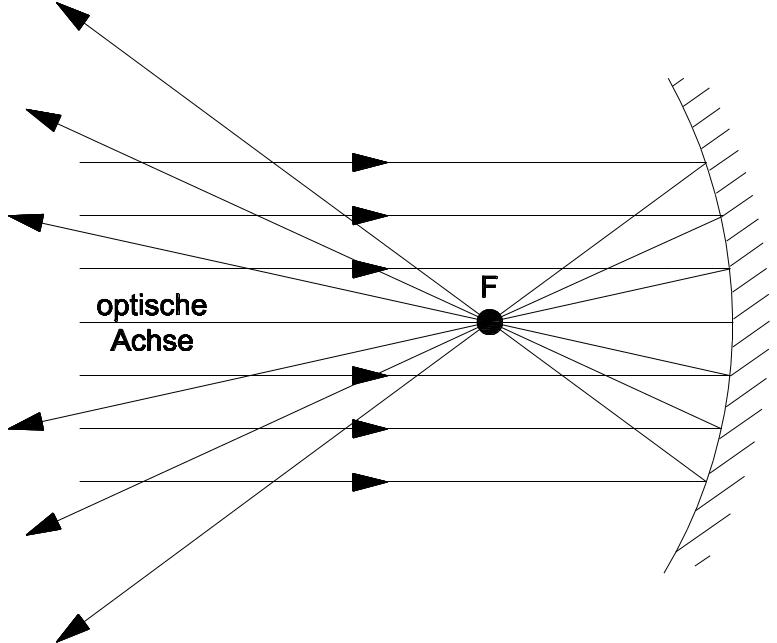
Bei sphärischen Spiegeln schneiden sich nur die achsennahen Strahlen exakt im Brennpunkt, so dass die Formeln auch nur für achsennahe Strahlen eine hinreichende Genauigkeit bieten.
Bilder des Hohlspiegels:
reell = direkte Projektion auf Oberfläche möglich; virtuell = Bild scheint hinter der Spiegelfläche zu liegen
#
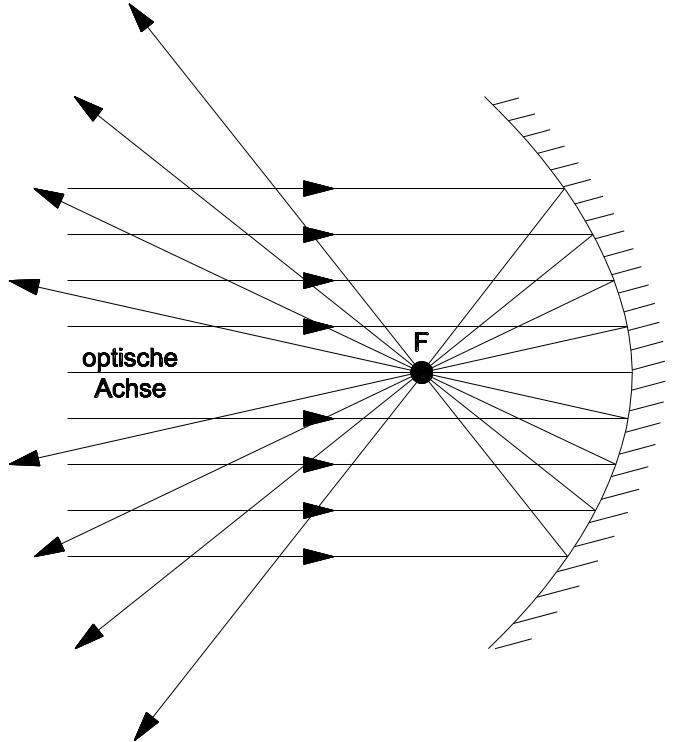
Parabolspiegel
Die Spiegeloberfläche eines Parabolspiegels hat die Form eines Paraboloids. Ein Paraboloid entsteht bei der Rotation einer Parabel um eine Achse. Ein Parabolspiegel ist ein asphärischer und symmetrischer Spiegel mit einem Brennpunkt. Durch die Parabolform schneiden sich auch die achsenfernen Strahlen im Brennpunkt des Spiegels, wodurch die Abbildungsqualität wesentlich verbessert wird. Parabolspiegel sind sphärischen Spiegeln sehr ähnlich.
#
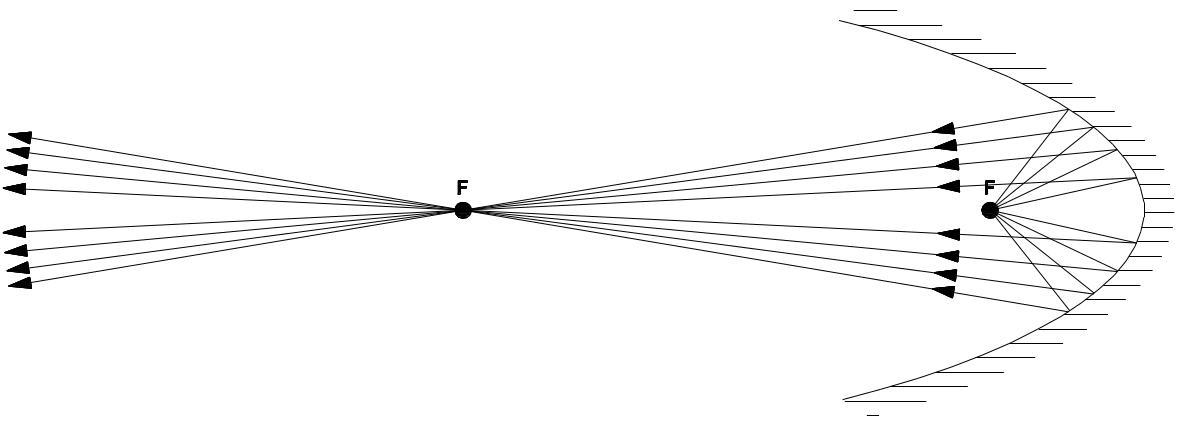
Ellipsenspiegel
Die Spiegeloberfläche eines Ellipsenspiegels ist elliptisch geformt und hat ähnliche Eigenschaften wie ein Parabolspiegel. Ellipsenspiegel besitzen jedoch einen zweiten nutzbaren Brennpunkt weit außerhalb des Spiegels. Der zweite Brennpunkt ermöglicht einen Einsatz des Ellipsenspiegels für Projektionszwecke. Aus diesem Grund werden Ellipsenspiegel häufig in Profilscheinwerfern eingesetzt.
#
Wölbspiegel (Konvexspiegel)
Wie bei einem Hohlspiegel hat die Flächennormale (Senkrechte zur Spiegelebene, Lot) für jeden Punkt der Spiegeloberfläche eine andere Richtung. Parallel zur optischen Achse auftreffende Strahlen werden so reflektiert, als kämen sie vom Brennpunkt F (auch als Zerstreuungspunkt bezeichnet). Es werden stets virtuelle, aufrechte und verkleinerte Bilder erzeugt. Es gelten dieselben Gleichungen wie für Hohlspiegel, jedoch mit dem Unterschied, dass die Brennweite f und die Bildweite b negativ sind, weil sie hinter dem Spiegel liegen.
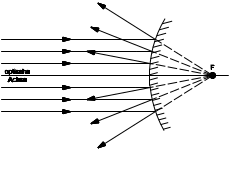
virtuell = Bild scheint hinter der Spiegelfläche zu liegen
#
Blenden
In jedem Linsensystem für Kameras (Optik, Objektiv) wird eine Iris verwendet, um die Menge des einfallenden Lichts zu regulieren. Die Öffnungsgröße der Iris wird über eine Blendenzahl (kurz: Blende) angegeben, die eine theoretische Menge des einfallenden Lichts in einem Linsensystem angibt. Im englischen Sprachraum wird die Blendenzahl als „f-number“ bezeichnet und üblicherweise mit „f-stop“ oder „stop“ abgekürzt. Die Blendenzahl wird ermittelt durch eine Division der Brennweite durch den Durchmesser der Linsenöffnung (Irisgröße). Die Blendenreihe basiert auf der Wurzel aus zwei (√2). Jede weitere Blendenzahl wird durch weiteres Multiplizieren von √2 ermittelt. Mit diesem System der Blendenreihe kann eine konsistente und in geometrischen Schritten verlaufende gleichmäßige Belichtung von Filmmaterialien erreicht werden. Jede Zahl wird als eine Blende (f-stop) bezeichnet. Der Kehrwert einer quadrierten Blendenzahl (1/f-stop2) gibt die Menge des einfallenden Lichts an.
Jeder Blendenschritt entspricht einer Verdoppelung oder Halbierung des einfallenden Lichts.
Typische Blendenzahlen sind: f1, f1.4, f2, f2.8, f4, f5.6, f8, f11, f16, f22, f32, f45
Die Blendenzahl f-stop hat einen rein mathematischen Ursprung. Reale Linsensysteme (Optiken) sind jedoch in ihren lichtleitenden Eigenschaften weniger effizient als deren mathematische Grundlagen. Insbesondere Zoomlinsen haben eine geringe Effizienz. Um den Effizienzverlust mit einzuberechnen, werden Linsensysteme vom Hersteller auf einer optischen Bank gemessen und entsprechend kalibriert. Der kalibrierte Blendenwert wird auch als t-stop oder t-number (Transmission Number) bezeichnet. Die meisten Linsensysteme sind in der Regel mit einer weißen f-stop- und einer roten t-stop-Skala versehen.
#
Tiefenschärfe*
Eine Veränderung der Blende bewirkt auch immer eine Veränderung der Tiefenschärfe. Eine Veränderung der Tiefenschärfe bedeutet eine Vergrößerung oder Verkleinerung des Tiefenbereichs, in dem Objekte scharf fokussiert sind. Die Tiefenschärfe hängt ebenfalls mit der Brennweite der Linse und dem Fokusbereich zusammen.
Eine Vergrößerung der Blende (Vergrößerung der Blendenzahl, Verkleinerung des Irisdurchmessers) vergrößert den Schärfebereich in der Tiefe (größere Tiefenschärfe) bei gleichzeitiger Verringerung der einfallenden Lichtmenge. Eine Verkleinerung der Blende (Verkleinerung der Blendenzahl, Vergrößerung des Irisdurchmessers) verkleinert den Schärfebereich in der Tiefe (geringe Tiefenschärfe) bei gleichzeitiger Vergrößerung der einfallenden Lichtmenge.
Bei Foto- oder Filmaufnahmen spielt die Tiefenschärfe eine große Rolle, da darüber das Verhältnis zwischen Vorder- und Hintergrund bestimmt werden kann. Bei kleiner Tiefenschärfe können leichte Farbunterschiede ineinander verlaufen und Details, Oberflächenmodelierung und Strukturen verloren gehen. Bei größeren Tiefenschärfen können durch Detailschärfe der Hintergrund oder Bildteile dominant werden und die Komposition des Gesamtbildes stören.
- Konstante Brennweite und Kamera-Objekt-Entfernung Die Vergrößerung der Blende (Verkleinerung des Irisdurchmessers) bei konstanter Brennweite und Kamera-Objekt-Entfernung bewirkt eine Vergrößerung der Tiefenschärfe.
* Der Begriff der Tiefenschärfe ist im eigentlichen Wortsinn nicht ganz richtig, hat sich jedoch Umgangssprachlich durchgesetzt. Die richtige Formulierung für dieses Phänomen müsste eigentlich Schärfentiefe sein. Blendet man bei einem Objektiv weiter ab, so wird der Bereich der Schärfe tiefer, d. h. die Schärfentiefe nimmt zu. Dies ist unabhängig von der Fokussierung auf die Nähe oder Ferne. Tiefenschärfe hingegen würde bedeuten, dass ein Foto in der Ferne (Tiefe) schärfer wird, was eben nur zutrifft, wenn auch in der Ferne fokussiert wurde.
Konstante Brennweite und Blende
Die Vergrößerung der Kamera-Objekt-Entfernung (Kamerafahrt) bei konstanter Brennweite und Blende bewirkt eine Vergrößerung der Tiefenschärfe. Der Bildausschnitt wird vergrößert bei gleichzeitiger Reduzierung der Objektgröße.Konstante Blende und Kamera-Objekt-Entfernung
Die Verkleinerung der Brennweite (Aufweiten des Linsenwinkels, Zoom) bei konstanter Blende und Kamera-Objekt-Entfernung bewirkt eine Vergrößerung der Tiefenschärfe. Der Bildausschnitt wird vergrößert bei gleichzeitiger Reduzierung der Objektgröße.
#
Abbildungsfehler
In einer fehlerfreien Abbildung ist jeder Bildpunkt eindeutig einem Gegenstandspunkt zuzuordnen. Ebenso muss die geometrische Anordnung der Bild- und Gegenstandspunkte ähnlich sein. Diese Bedingungen werden von sphärischen Linsen jedoch nur annähernd erfüllt. Die Abweichungen von den Bedingungen werden als Abbildungsfehler bezeichnet, die als folgende Effekte auftreten können.
Sphärische Abberation
Die Brennweite ist für Strahlen nahe der optischen Achse kleiner als für achsenferne Strahlen, wodurch Abbildungsfehler durch unterschiedliche Brennpunkte entstehen. Eine Abhilfe schafft die Abgrenzung von achsenfernen Lichtstrahlen (Blenden), wobei jedoch ein Helligkeitsverlust resultiert.Chromatische Abberation
Aufgrund verschiedener Brennweiten der unterschiedlichen Wellenlänge im sichtbaren weißen Licht kommt es zu unscharfen Bildern mit farbigen Rändern. Ursache hierfür ist die Dispersion von Lichtstrahlen an den Grenzen von Medien verschiedener Dichte. Der Fehler kann vermieden werden durch die Kombination einer Sammellinse aus Kronglas mit einer Zerstreuungslinse aus Flintglas, die als achromatisches Linsenpaar bzw. Achromat bezeichnet wird. Achromatische Linsenpaare können jedoch nur die Farbfehler von zwei bestimmten Wellenlängen korrigieren.Astigmatismus
Sammellinsen mit zwei verschiedenen zueinander senkrecht stehenden Krümmungsradien brechen auf die Linse auftreffende Lichtstrahlen verschieden stark, so dass zwei Brennpunkte entstehen. Es resultiert ein verzerrtes und unscharfes Bild. Dieser Effekt tritt auch auf, sofern die Krümmungsradien beider Seiten einer Sammellinse gleich sind, aber die Strahlen von einer Lichtquelle kommen, die seitlich von der optischen Achse liegt.Bildfeldwölbung
Das Bild wird auf einer gewölbten Fläche abgebildet, wobei eine Randunschärfe entsteht. Der Fehler wird vermieden durch den Einsatz besonderer Linsensysteme, den sog. Aplanaten.Verzeichnung
Tonnen- bzw. kissenförmige Verzerrungen des Bildes, d. h., vor allen an den Rändern des Bildes werden die Geraden nach innen oder außen gekrümmt.Koma
Strahlenbündel großer Öffnung bilden einen Punkt außerhalb der optischen Achse als ovale Figur mit kometenhaften Schweif ab.
Abbildungsfehler können durch Kombination verschiedener Linsen mit unterschiedlichen Glassorten sowie Blenden und Variationen der Linsenform (z. B. asphärische Linsen) korrigiert werden.
#
Auflösungsvermögen
Das Auflösungsvermögen optischer Geräte ist durch die physikalischen Phänomene der Beugung bzw. Interferenz von Lichtstrahlen an Blenden und Objektivöffnungen begrenzt. Es entstehen Interferenzscheiben und -ringe, die sich benachbarten Bildpunkten überlagern und damit eine Unschärfe erzeugen. Gegenstandspunkte werden nicht als Punkte, sondern als kleine Scheibchen abgebildet, die sich gegenseitig überdecken und deshalb nicht mehr getrennt wahrgenommen werden können.
Zwei Punkte können noch voneinander unterschieden werden, wenn der Winkel (Epsilon), unter dem sie beobachtet werden, mindestens folgender Formel entspricht:
\epsilon \approx sin \epsilon \geq 1,22 \frac{\lambda}{d}ε = Betrachtungswinkel
λ = Wellenlänge des Lichts
d = Durchmesser der Objektivöffnung bzw. Blende
Das Auflösungsvermögen wird umso besser, je kleiner die verwendete Wellenlänge und je größer der Blendendurchmesser ist. Für das menschliche Auge entspricht die Grenze des Auflösungsvermögens einem Betrachtungswinkel von einer Bogenminute (1 Bogenminute = 1/60 Grad).
#
Vergütung optischer Systeme
An der Oberfläche von Objektiv-Linsen werden bis zu 5 % des in einem Bereich von 4° bis 10° einfallenden Lichts reflektiert. Hochwertige Objektive bestehen aus einem Linsensystem mit mehreren Linsen, in denen sich die Reflektionen an den einzelnen Linsenoberflächen aufsummieren. Es entstehen beträchtliche Transmissionsverluste, störendes Streulicht und Geisterbilder. Um diese Verluste und Artefakte zu minimieren, werden mit Hilfe des Interferenz-Effektes optische Systeme entspiegelt (vergütet).
Um ganze Wellenlängenbereiche des sichtbaren Lichts zu entspiegeln, werden mehrere dünne Schichten einer Oxydverbindung auf die Linsenoberfläche aufgebracht. An den Übergängen zwischen den einzelnen Schichten und der Linse kommt es zu Mehrfachreflexionen, die einen Laufwegunterschied von /2 zwischen den reflektierten Wellenlängen zur Folge haben. Die Gangunterschiede bewirken ein gegenseitiges Aufheben der reflektierten Wellenlängen. Reflexionen an Linsenoberflächen können mit diesem Verfahren nahezu beseitigt werden.