#
Mechanik

Definition:
- Mechanik: In der Mechanik werden Kräfte und Belastungen von ruhenden und sich bewegenden Körpern berechnet.
- Statik: Die Statik beschreibt das Kräfteverhältnis von Körpern im Ruhezustand.
- Dynamik: Die Dynamik beschreibt die Bewegung von Körpern als Ursache von Krafteinwirkung.
- Körper: Körper sind alle Objekte, die durch Masse, Position und Volumen gekennzeichnet werden können.
- Kraft: Die Einwirkung einer Kraft ist die Ursache für eine Bewegung, Bewegungsänderung oder eine Deformation. Ruhende Gegenstände verbleiben durch eine Kraft an Ort und Stelle. Kräfte haben eine Richtung und eine Größe. Sie werden mathematisch als Vektoren (Richtung und Betrag) ausgedrückt. Die Kraft (Force F) ist das Produkt aus Masse (kg) und Beschleunigung (a = m/s2). Die Einheit der Kraft ist Newton (N = kg*m/s2). Dieser Zusammenhang wird auch als Grundgesetz der Mechanik bezeichnet (F = m × a).
- Gravitation: Die Erdanziehung (Gravitation) wird auch Fallbeschleunigung genannt und ist eine Gewichtskraft, die überall auf der Erde eine konstante Größe von N = 9,81 kg*m/s2 hat und durch die Masse der Erde verursacht wird.
#
Grundlagen der Statik
#
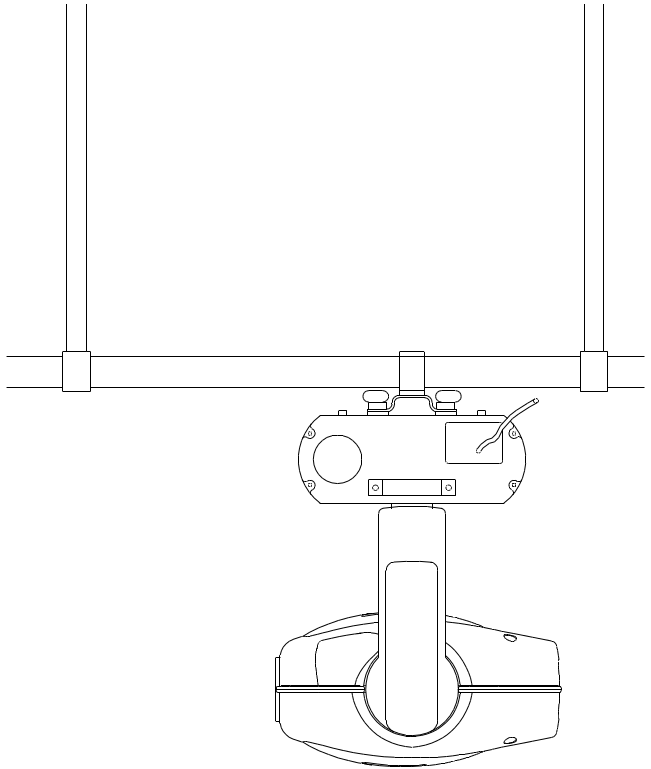
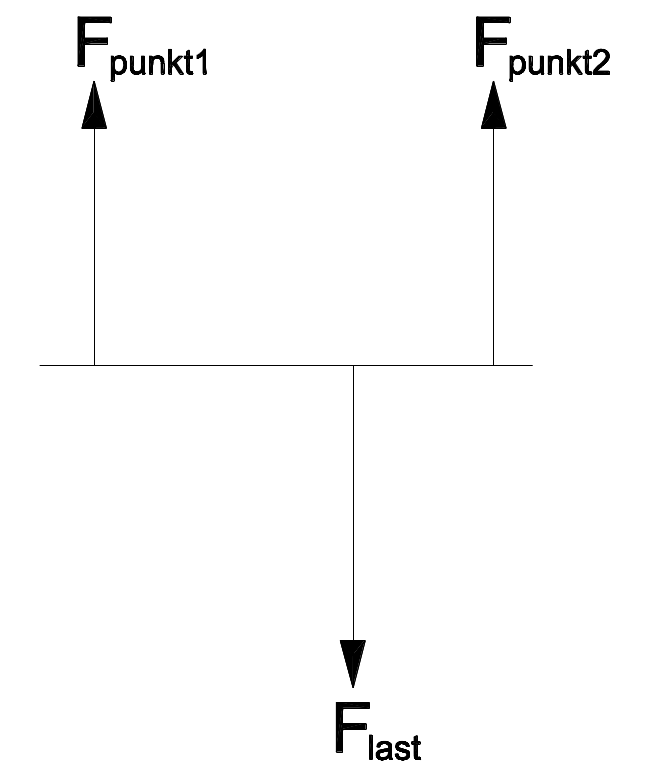
Freistellen von Kräften
Jedes beliebige mechanische System kann in seine Einzelkräfte zerlegt werden. Beim Freistellen werden alle im System wirkenden Kräfte entsprechend ihrer Wirkungsrichtung in Vektoren mit Betrag und Richtung dargestellt. Anhand dieser Vektoren lassen sich Kräfteverhältnisse berechnen.
#
Kräfte auf einer Wirkungslinie
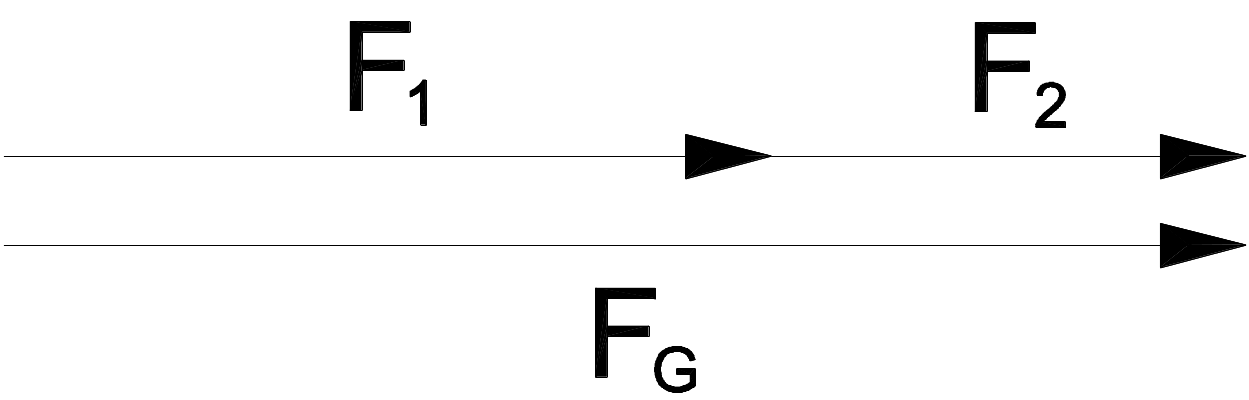
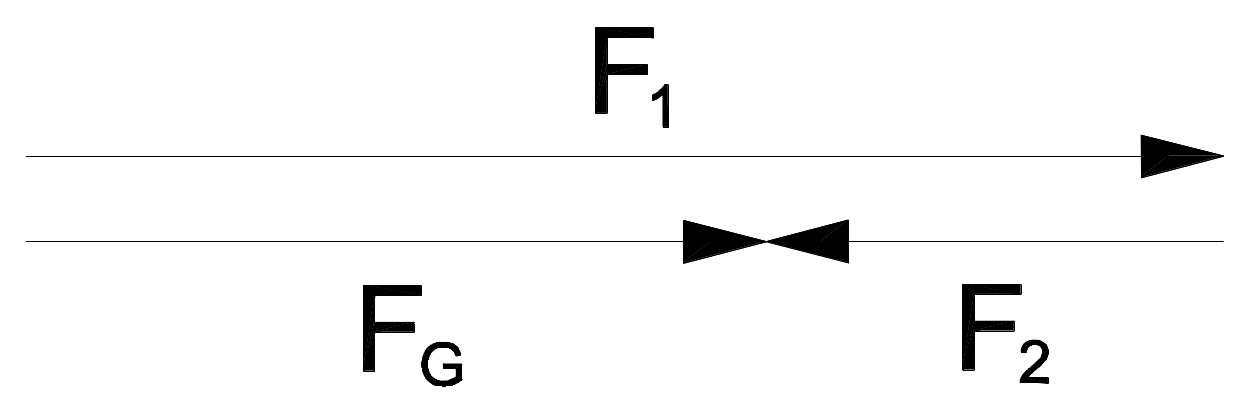
F_G = F_1 \plusmn F_2
F_G = \sum F_n
#
Kräfte auf einer Wirkungslinie mit beliebigen Richtungen
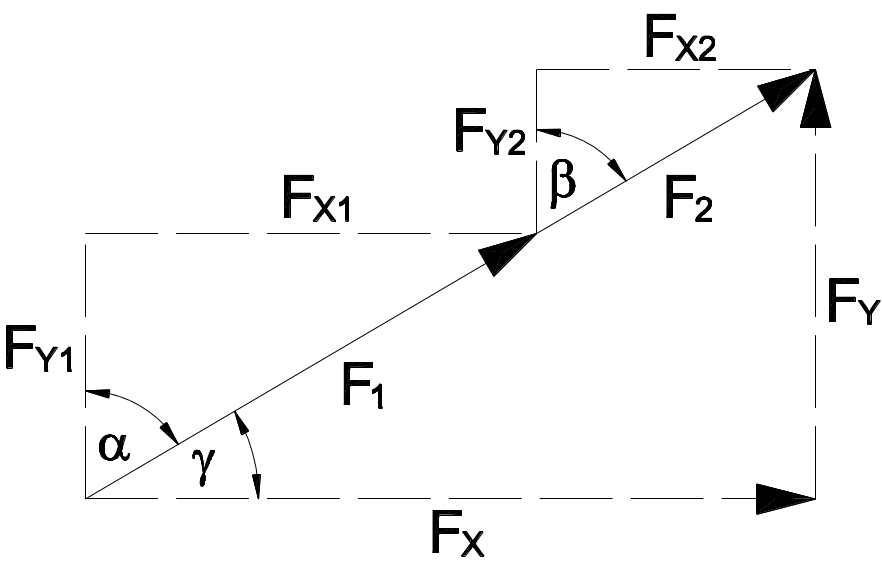
F_X = F_{X1} \plusmn F_{X2}F_Y = F_{Y1} \plusmn F_{Y2}\sin \alpha = \frac{F_{X1}}{F_1}F_{X1} = \sin \alpha \times F_1\cos \alpha = \frac{F_{Y1}}{F_1}F_{Y1} = \cos \alpha \times F_1F_G = \sqrt{({F_X}^2) + ({F_Y}^2)}\tan \gamma = \frac{F_Y}{F_X}\sin \beta = \frac{F_{X2}}{F_2}F_{X2} = \sin \beta \times F_2\cos \beta = \frac{F_{Y2}}{F_2}F_{Y2} = \cos \beta \times F_2
#
Zentrales Kräftesystem mit beliebigen Richtungen*
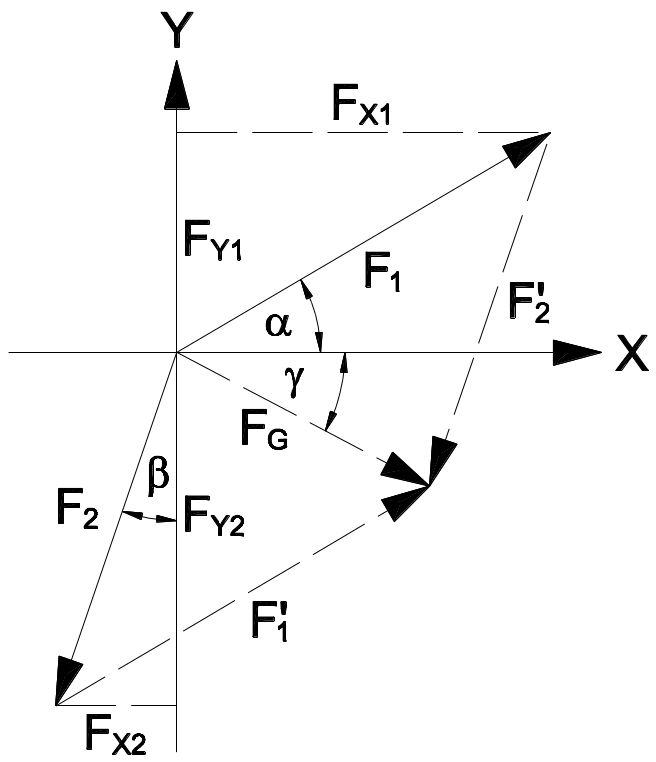
\cos \alpha = \frac{F_{X1}}{F_1}F_{X1} =\cos \alpha \times F_1\sin \alpha = \frac{F_{Y1}}{F_1}F_{Y1} =\sin \alpha \times F_1\sin \beta = \frac{-F_{X2}}{F_2}-F_{X2} = \sin \beta \times F_2\cos \beta = \frac{-F_{Y2}}{F_2}-F_{Y2} = \cos \beta \times F_2F_X = F_{X1} - F_{X2}F_Y = F_{Y1} - F_{Y2}F_G = \sqrt{({F_X}^2) + ({F_Y}^2)}\tan \gamma = \frac{F_{YG}}{F_{XG}}* In einem zentralen Kräftesystem kann die Gesamtkraft FG auch durch Parallelverschiebung der Einzelkräfte in einer zeichnerischen Lösung ermittelt werden.
#
Gleichgewichtbedingungen im zentralen Kräftesystem
Ein in Ruhe befindliches zentrales Kräftesystem ist im Gleichgewichtszustand. Die Summe aller an einen Punkt angreifenden Kräfte ist dabei gleich Null. Für den Gleichgewichtszustand sind Haltekräfte (Auflagekräfte) notwendig. Befindet sich ein System nicht im Gleichgewichtszustand, bewirkt die stärkste Kraft eine Bewegung der Masse. Greifen Kräfte aus verschiedenen Richtungen in einem zentralen Kräftesystem an, müssen im Ruhezustand die Kräfte der einzelnen Richtungen im Gleichgewicht stehen. Über die Gleichgewichtsbedingung können alle auftretenden Kräfte berechnet werden.
\sum F_G = 0 \quad \quad \quad \sum F_X = 0 \quad \quad \quad \sum F_Y = 0
#
Gleichgewichtbedingungen im allgemeinen Kräftesystem
Bei allgemeinen Kräftesystemen greifen Kräfte nicht am gleichen Punkt an. Wenn die Wirkungslinien zweier Kräfte parallel verlaufen und die Kräfte einen ungleichen Betrag haben oder entgegengesetzt sind, entstehen so genannte Momente (Dreh-, Kipp- und Biegemomente). Durch das parallele Angreifen der Wirkungslinien ergibt eine Verdrehung (Rotation) des Körpers um einen Drehpunkt bei gleichzeitigem Gleichgewichtszustand in X- und Y-Richtung. Die Drehung (Kippung, Biegung) des Körpers beruht auf einem durch das Kräftepaar erzeugten Moment. Der Betrag des Moments (M) ist von dem Wirkabstand (a) und der angreifenden Kraft (F) abhängig.
M = F \times a
Ist ein allgemeines Kräftesystem im Gleichgewichtszustand, sind die Summen aller Kräfte und die Summe aller Momente an einem Punkt gleich null.
\sum F_G = 0 \quad \quad \sum F_X = 0 \quad \quad \sum F_Y = 0 \quad \quad \sum M_{(\text{Punkt X})} = 0Jede angreifende Kraft erzeugt einen Moment. Der zu betrachtende Drehpunkt kann frei definiert werden und dient bei der Summierung der Momente als Basispunkt. Bei der Aufsummierung der Momente muss eine einheitliche Drehrichtung um den Basispunkt beachtet werden. Der Betrag eines Einzelmoments ist abhängig vom Wirkabstand (Abstand vom Drehpunkt a) und der senkrecht zum Drehhebel auftretenden Kraftkomponente.
Beispiel:*
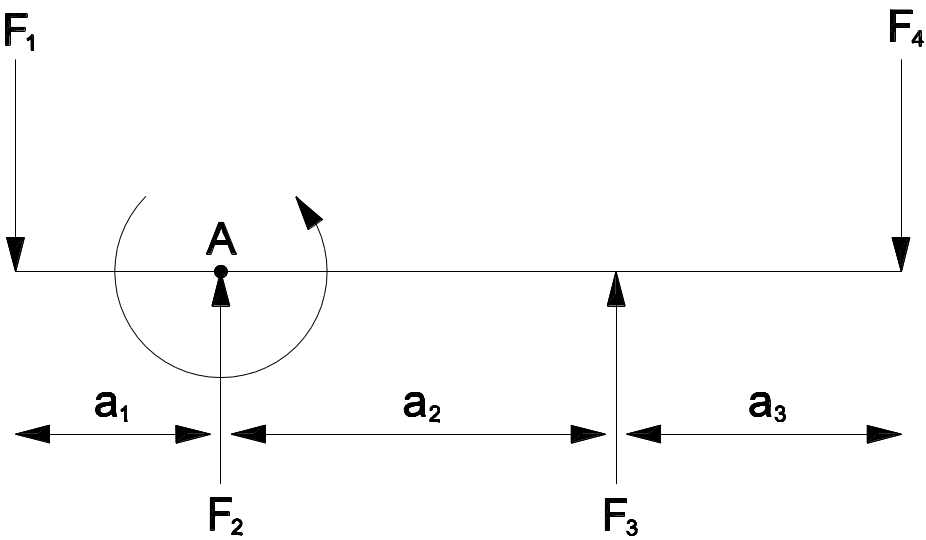
\sum F_X = 0
\sum F_Y = 0 = -F_1 + F_2 + F_3 - F_4
\sum M_A = 0 = F_1 \times \alpha _1 + F_3 \times \alpha _2 -F_4(a_2 + a_3)
* Über die Gleichgewichtsbedingungen können bei zwei bekannten Kräften die unbekannten Kräfte berechnet werden.
#
Gleichgewichtbedingungen mit Streckenlasten
Über eine Länge erstreckte Lasten bezeichnet man als Streckenlasten. Bei Streckenlasten wirkt eine Kraft auf eine Längeneinheit ein (kN pro Meter). Streckenlasten lassen sich für eine einfachere Berechnung in eine Auflagekraft umwandeln. Dabei wird die Streckenlast mit der Länge der Krafteinwirkung multipliziert. Die resultierende Auflagekraft liegt in der Mitte der Streckenlast. Auftretende Kräfte können über die bekannten Gleichgewichtsbedingungen berechnet werden.
#
Berechnung von Bridle-Längen
Beim Anschlagen von Traversen oder Gewichten kann es notwendig werden, einen Hängepunkt zwischen zwei vorhandenen Hängepunkten zu setzen. Diese Technik wird als Bridle bezeichnet und ist eine improvisierte Alternative zu einem Träger, der die auftretenden Kräfte in das Dach weiterleitet. Durch das schräge Anschlagen der Last ist die Tragfähigkeit des Hängepunktes vom Winkel und der Länge der Bridle-Stränge abhängig. Nach BGV C1 und VBG 9a muss der Innenwinkel kleiner als 120° sein. Ebenso dürfen nur Stahlseile mit einem Sicherheitsfaktor von 12 verwendet werden. Die vorhandenen Hängepunkte dürfen weder horizontal noch vertikal überlastet werden.
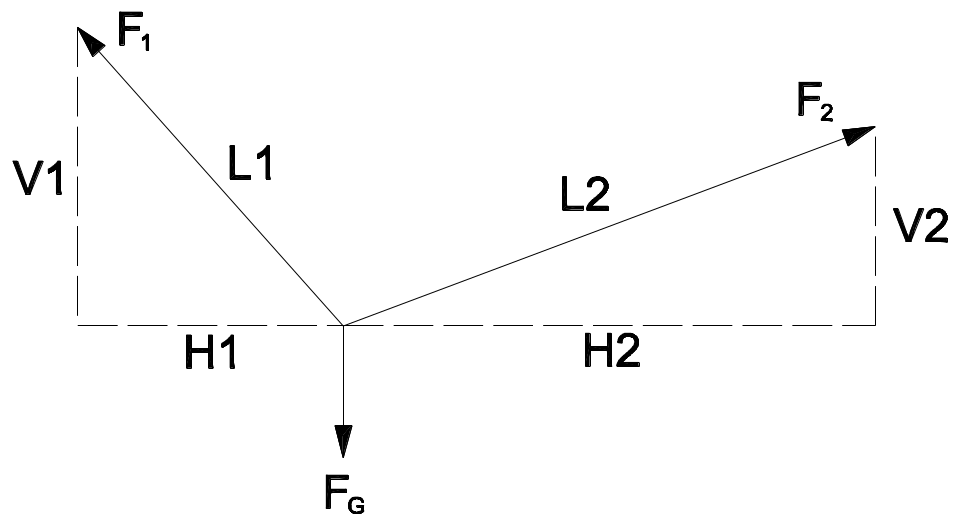
L1^2 = V1^2 + H1 {#2}L1 = \sqrt{V1^2 + H1^2}L2^2 = V2^2 + H2 {#2}L2 = \sqrt{V2^2 + H2^2}
#
Berechnung von Bridle-Kräften
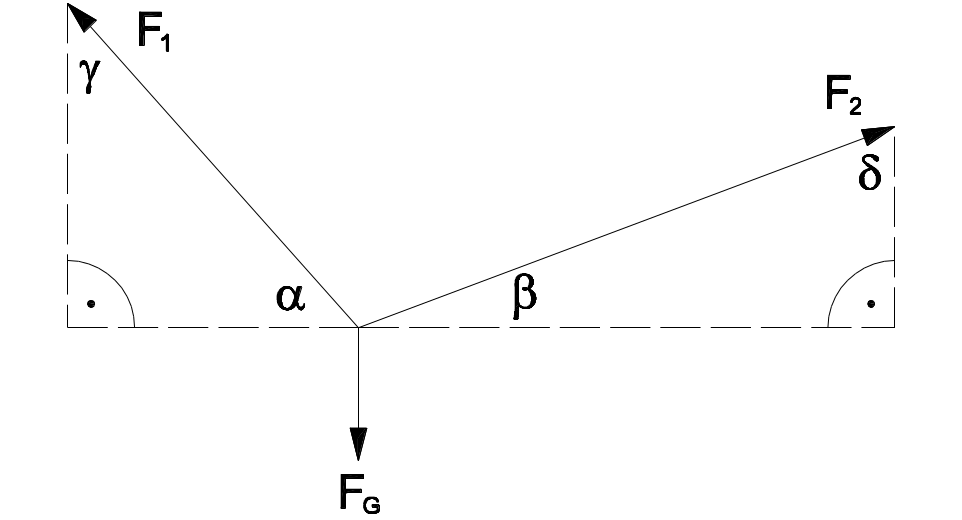
\alpha = 90° - \gamma
\beta = 90° - \delta
F_1 = \frac{1}{\sin \alpha + (cos \alpha \times \tan \beta)} \times F_GF_2 = \frac{1}{\sin \beta + (cos \beta \times \tan \alpha)} \times F_G
#
Tabelle zur Bridle-Kraft F1
F_1 = \text{Tabellenwart} \times F_G| Winkel | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | |
| 5 | 5,737 | 3,805 | 2,824 | 2,224 | 1,813 | 1,510 | 1,274 | 1,083 | 0,923 | 0,785 | 0,662 | 0,552 | 0,450 | 0,354 | 0,263 | 0,174 | 0,087 | 0,000 |
| 10 | 3,849 | 2,879 | 2,286 | 1,879 | 1,580 | 1,347 | 1,158 | 1,000 | 0,863 | 0,742 | 0,633 | 0,532 | 0,438 | 0,347 | 0,260 | 0,174 | 0,087 | 0,000 |
| 15 | 2,913 | 2,330 | 1,932 | 1,638 | 1,410 | 1,225 | 1,069 | 0,935 | 0,816 | 0,709 | 0,610 | 0,518 | 0,429 | 0,343 | 0,259 | 0,174 | 0,089 | 0,000 |
| 20 | 2,357 | 1,970 | 1,684 | 1,462 | 1,282 | 1,131 | 1,000 | 0,885 | 0,780 | 0,684 | 0,594 | 0,508 | 0,424 | 0,342 | 0,260 | 0,176 | 0,090 | 0,000 |
| 25 | 1,992 | 1,717 | 1,503 | 1,329 | 1,183 | 1,057 | 0,946 | 0,845 | 0,752 | 0,665 | 0,582 | 0,502 | 0,423 | 0,343 | 0,263 | 0,180 | 0,093 | 0,000 |
| 30 | 1,737 | 1,532 | 1,366 | 1,227 | 1,106 | 1,000 | 0,904 | 0,815 | 0,732 | 0,653 | 0,576 | 0,500 | 0,424 | 0,347 | 0,268 | 0,185 | 0,096 | 0,000 |
| 35 | 1,550 | 1,393 | 1,261 | 1,147 | 1,047 | 0,956 | 0,872 | 0,793 | 0,718 | 0,645 | 0,574 | 0,502 | 0,429 | 0,354 | 0,275 | 0,192 | 0,101 | 0,000 |
| 40 | 1,409 | 1,286 | 1,179 | 1,085 | 1,000 | 0,922 | 0,848 | 0,778 | 0,710 | 0,643 | 0,576 | 0,508 | 0,438 | 0,364 | 0,286 | 0,201 | 0,106 | 0,000 |
| 45 | 1,300 | 1,202 | 1,115 | 1,037 | 0,964 | 0,897 | 0,832 | 0,769 | 0,707 | 0,645 | 0,582 | 0,518 | 0,450 | 0,377 | 0,299 | 0,212 | 0,114 | 0,000 |
| 50 | 1,216 | 1,137 | 1,066 | 1,000 | 0,938 | 0,879 | 0,822 | 0,766 | 0,710 | 0,653 | 0,594 | 0,532 | 0,466 | 0,395 | 0,316 | 0,227 | 0,123 | 0,000 |
| 55 | 1,150 | 1,087 | 1,028 | 0,973 | 0,920 | 0,869 | 0,819 | 0,769 | 0,718 | 0,665 | 0,610 | 0,552 | 0,488 | 0,418 | 0,338 | 0,246 | 0,136 | 0,000 |
| 60 | 1,099 | 1,048 | 1,000 | 0,954 | 0,910 | 0,866 | 0,822 | 0,778 | 0,732 | 0,684 | 0,633 | 0,577 | 0,516 | 0,446 | 0,366 | 0,270 | 0,152 | 0,000 |
| 65 | 1,060 | 1,020 | 0,981 | 0,943 | 0,906 | 0,869 | 0,832 | 0,793 | 0,752 | 0,709 | 0,662 | 0,610 | 0,552 | 0,484 | 0,403 | 0,303 | 0,174 | 0,000 |
| 70 | 1,031 | 1,000 | 0,970 | 0,940 | 0,910 | 0,879 | 0,848 | 0,815 | 0,780 | 0,742 | 0,700 | 0,653 | 0,598 | 0,532 | 0,451 | 0,347 | 0,206 | 0,000 |
| 75 | 1,012 | 0,989 | 0,966 | 0,943 | 0,920 | 0,897 | 0,872 | 0,845 | 0,816 | 0,785 | 0,749 | 0,707 | 0,657 | 0,596 | 0,518 | 0,411 | 0,255 | 0,000 |
| 80 | 1,000 | 0,985 | 0,970 | 0,954 | 0,938 | 0,922 | 0,904 | 0,885 | 0,863 | 0,839 | 0,811 | 0,778 | 0,737 | 0,684 | 0,612 | 0,508 | 0,337 | 0,000 |
| 85 | 0,996 | 0,989 | 0,981 | 0,973 | 0,964 | 0,956 | 0,946 | 0,935 | 0,923 | 0,909 | 0,892 | 0,872 | 0,845 | 0,809 | 0,757 | 0,671 | 0,502 | 0,000 |
| 90 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,500 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | |
#
Tabelle zur Bridle-Kraft F2
F_2 = \text{Tabellenwart} \times F_G| Winkel | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | |
| 5 | 5,737 | 3,849 | 2,913 | 2,357 | 1,992 | 1,737 | 1,550 | 1,409 | 1,300 | 1,216 | 1,150 | 1,099 | 1,060 | 1,031 | 1,012 | 1,000 | 0,996 | 1,000 |
| 10 | 3,805 | 2,879 | 2,330 | 1,970 | 1,717 | 1,532 | 1,393 | 1,286 | 1,202 | 1,137 | 1,087 | 1,048 | 1,020 | 1,000 | 0,989 | 0,985 | 0,989 | 1,000 |
| 15 | 2,824 | 2,286 | 1,932 | 1,684 | 1,503 | 1,366 | 1,261 | 1,179 | 1,115 | 1,066 | 1,028 | 1,000 | 0,981 | 0,970 | 0,966 | 0,970 | 0,981 | 1,000 |
| 20 | 2,224 | 1,879 | 1,638 | 1,462 | 1,329 | 1,227 | 1,147 | 1,085 | 1,037 | 1,000 | 0,973 | 0,954 | 0,943 | 0,940 | 0,943 | 0,954 | 0,973 | 1,000 |
| 25 | 1,813 | 1,580 | 1,410 | 1,282 | 1,183 | 1,106 | 1,047 | 1,000 | 0,964 | 0,938 | 0,920 | 0,910 | 0,906 | 0,910 | 0,920 | 0,938 | 0,964 | 1,000 |
| 30 | 1,510 | 1,347 | 1,225 | 1,131 | 1,057 | 1,000 | 0,956 | 0,922 | 0,897 | 0,879 | 0,869 | 0,866 | 0,869 | 0,879 | 0,897 | 0,922 | 0,956 | 1,000 |
| 35 | 1,274 | 1,158 | 1,069 | 1,000 | 0,946 | 0,904 | 0,872 | 0,848 | 0,832 | 0,822 | 0,819 | 0,822 | 0,832 | 0,848 | 0,872 | 0,904 | 0,946 | 1,000 |
| 40 | 1,083 | 1,000 | 0,935 | 0,885 | 0,845 | 0,815 | 0,793 | 0,778 | 0,769 | 0,766 | 0,769 | 0,778 | 0,793 | 0,815 | 0,845 | 0,885 | 0,935 | 1,000 |
| 45 | 0,923 | 0,863 | 0,816 | 0,780 | 0,752 | 0,732 | 0,718 | 0,710 | 0,707 | 0,710 | 0,718 | 0,732 | 0,752 | 0,780 | 0,816 | 0,863 | 0,923 | 1,000 |
| 50 | 0,785 | 0,742 | 0,709 | 0,684 | 0,665 | 0,653 | 0,645 | 0,643 | 0,645 | 0,653 | 0,665 | 0,684 | 0,709 | 0,742 | 0,785 | 0,839 | 0,909 | 1,000 |
| 55 | 0,662 | 0,633 | 0,610 | 0,594 | 0,582 | 0,576 | 0,574 | 0,576 | 0,582 | 0,594 | 0,610 | 0,633 | 0,662 | 0,700 | 0,749 | 0,811 | 0,892 | 1,000 |
| 60 | 0,552 | 0,532 | 0,518 | 0,508 | 0,502 | 0,500 | 0,502 | 0,508 | 0,518 | 0,532 | 0,552 | 0,577 | 0,610 | 0,653 | 0,707 | 0,778 | 0,872 | 1,000 |
| 65 | 0,450 | 0,438 | 0,429 | 0,424 | 0,423 | 0,424 | 0,429 | 0,438 | 0,450 | 0,466 | 0,488 | 0,516 | 0,552 | 0,598 | 0,657 | 0,737 | 0,845 | 1,000 |
| 70 | 0,354 | 0,347 | 0,343 | 0,342 | 0,343 | 0,347 | 0,354 | 0,364 | 0,377 | 0,395 | 0,418 | 0,446 | 0,484 | 0,532 | 0,596 | 0,684 | 0,809 | 1,000 |
| 75 | 0,263 | 0,260 | 0,259 | 0,260 | 0,263 | 0,268 | 0,275 | 0,286 | 0,299 | 0,316 | 0,338 | 0,366 | 0,403 | 0,451 | 0,518 | 0,612 | 0,757 | 1,000 |
| 80 | 0,174 | 0,174 | 0,174 | 0,176 | 0,180 | 0,185 | 0,192 | 0,201 | 0,212 | 0,227 | 0,246 | 0,270 | 0,303 | 0,347 | 0,411 | 0,508 | 0,671 | 1,000 |
| 85 | 0,087 | 0,087 | 0,089 | 0,090 | 0,093 | 0,096 | 0,101 | 0,106 | 0,114 | 0,123 | 0,136 | 0,152 | 0,174 | 0,206 | 0,255 | 0,337 | 0,502 | 1,000 |
| 90 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,500 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | |