#
Mathematischen Grundlagen

#
Mathematische Zeichen
#
Grundrechenarten
#
Brüche
\displaystyle \frac{3}{7} ---> Echter Bruch (Zähler < Nenner)
\displaystyle \frac{12}{7} ---> Unechter Bruch (Zähler > Nenner)
\displaystyle 2\frac{3}{7} ---> Gemischte Zahl (Ganze Zahl und Bruch)
\displaystyle \frac{1}{7} \frac{3}{7} \frac{5}{7} ---> Gleichnamige Brüche (Nenner gleich)
\displaystyle \frac{2}{5} \frac{3}{7} \frac{7}{9} ---> Ungleichnamige Brüche (Nenner ungleich)
#
Addieren und Subtrahieren von Brüchen
Gleichnamige Brüche:
\displaystyle \frac{1}{7} + \frac{3}{7} + \frac{5}{7} = \frac{9}{7} = 1\frac{2}{7} ---> Alle Brüche addieren/subtrahierenUngleichnamige Brüche:
\displaystyle \frac{2}{3} + \frac{3}{4} = \frac{8}{12} + \frac{9}{12} = \frac{17}{12} = 1\frac{5}{12} ---> Hauptnenner bilden, dann addieren/subtrahieren
#
Multiplizieren und Dividieren von Brüchen
\displaystyle \frac{5}{6} \times 3 = 5 \times \frac{3}{6} = \frac{15}{6} = 2 \frac{1}{2} ---> [ × ] Ganze Zahl mit Zähler multiplizieren
\displaystyle \frac{1}{8} \times \frac{4}{5} = \frac{1 \times 4}{8 \times 5} = \frac{4}{40} = \frac{1}{10} ---> [ × ] Zähler × Zähler, Nenner × Nenner
\displaystyle \frac{8}{9} \div 4 = \frac{8}{9 \times 4} = \frac{8}{36} = \frac{2}{9} ---> [ ÷ ] Ganze Zahl mit Nenner multiplizieren
\displaystyle \frac{3}{8} \times \frac{4}{5} = \frac{3 \times 5}{8 \times 4} = \frac{15}{32} ---> [ ÷ ] Multiplizieren mit dem Kehrwert
#
Prozent
Grundwert ÷ 100 = Prozentwert (1% von Grundwert)
Prozentsatz = (100 × Prozentwert) ÷ Grundwert
#
Promille
Grundwert ÷ 1.000.000 = Promillewert (1‰ vom Grundwert)
#
Algebra
#
Kommutativgesetz
a + b = b + a
a \times b = b \times a
#
Assoziativgesetz
(a + b) +c =a + (b + c)
(a \times b) \times c = a \times (b \times c)
#
Distributivgesetz
a \times (b + c) = (a \times b) + (a \times c)
a \times (b - c) = (a \times b) - (a \times c)
(a + b) \times c = (a \times c) + (b \times c)
(a - b) \times c = (a \times c) - (b \times c)
#
I. Binomische Formel
(a + b)^2 = a^2 + 2ab + b^2
#
II. Binomische Formel
(a - b)^2 = a^2 - 2ab + b^2
#
III. Binomische Formel
(a + b) \times (a - b) = a^2 - b^2
#
Potenzen
a \times a \times \times … = a^n
a = Basis,
n = Exponent (Anzahl von a)
gilt nur für a ≠ 0
a^0 = 1
#
Potenzrechnung
a^{-n} = \frac{1}{a^n}
(a^m)^n = a^{m \times n}
a^m \times a^n = a^{m+n} --->[ × ] gleiche Basis
\frac{a^m}{a^n} = a^m \times \frac{1}{a^n} = a^{m-n} ---> [ ÷ ] gleiche Basis
a^n \times b^n = (a \times b)^n ---> [ × ] gleicher Exponent
\frac{a^n}{b^n} = (\frac{a}{b})^n ---> [ ÷ ] gleicher Exponent
#
Wurzeln
a^n = c ==> a = \sqrt[n]{c}
a = Wurzel
n = Wurzelexponent
c = Radikant
\sqrt[4]{5} + \sqrt[4]{5} = 2 \times \sqrt[4]{5}
nur möglich, wenn n und c gleich (gilt für Addition und Subtraktion)
\sqrt{3} \times \sqrt{2} = \sqrt{3 \times 2} = \sqrt{6}
\sqrt{4} \div \sqrt{2} = \sqrt{4 \div 2} = \sqrt{2}
#
Logarithmen
\log_{10}a = \lg\ a ---> dekadischer Logarithmus (Basis 10)
\log_ea = \ln\ a ---> natürlicher Logarithmus (Basis e)
\log_2a = lb\ a ---> binärer Logarithmus (Basis 2)
z = \log_x a \leftrightarrow x^z = a ---> a, x > 0; x \ne 1
log_x 1 = 0 ; log_x x = 1
#
Log. Multiplikation:
\log_x (a \times b) = \log_x a + \log_x b ---> a, b, x > 0; x \ne 1
#
Log. Division:
\log_x (a \div b) = \log_x a - \log_x b ---> a, b, x > 0; x \ne 1
#
Log. Potenzen:
\log_x (a^n) = n \times \log_x a ---> a, x > 0; x \ne 1; n > 1
#
Log. Wurzeln:
\log_x (\sqrt[n]{a}) = \frac{1}{n} \times \log_x a ---> a, x > 0; x \ne 1; n > 1
#
Geometrie
Die Winkelkonstante π gibt das Verhältnis von Umfang zu Durchmesser eines beliebigen Kreises an.
#
Winkeleinheiten
#
Bogenmaß (Radiant)
Ein Winkel wird mit der Einheit Radiant (rad) bezeichnet, wenn die Größe des Winkels durch das Verhältnis der Bogenlänge zum Kreisradius ermittelt wird.
1 \ Vollwinkel = 2 \times \pi \ rad
#
Grad (Altgrad)
1 Grad (°) ist der 360ste Teil eines Vollwinkels (2 × π rad) und wird in 60 Minuten (’) oder 3600 Sekunden (“) unterteilt.
1 \deg = \frac{1}{360rad} \times 2\pi = \frac{\pi}{180rad}
#
Gon (Neugrad)
1 Gon ist der 400ste Teil eines Vollwinkels (2 × π rad) und wird in 100 cgon oder 1000 mgon unterteilt.
1gon = \frac{1}{400rad} \times 2\pi = \frac{\pi}{200rad}
#
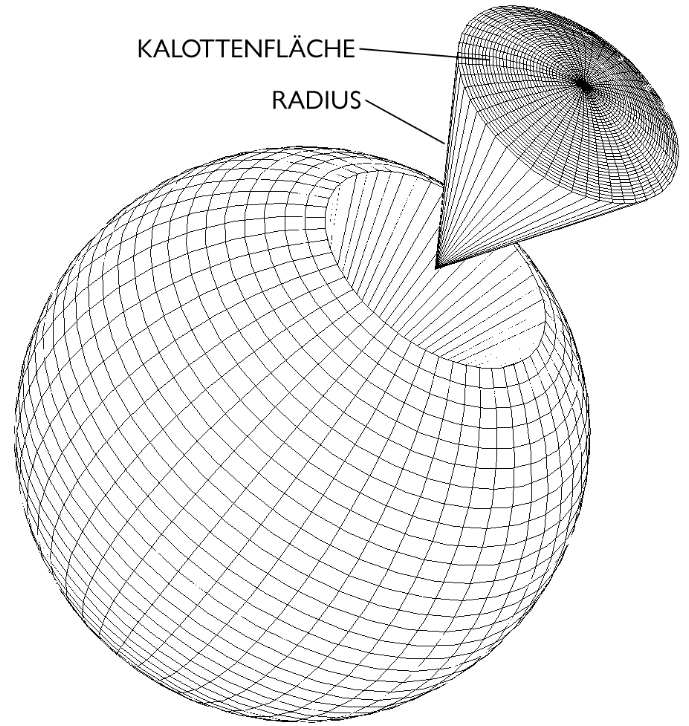
Raumwinkel (Steradiant)
Unter dem Raumwinkel versteht man den Quotienten aus dem Flächeninhalt eines Teilstücks einer Kugeloberfläche A (Kalottenfläche) und dem Quadrat des zugehörigen Kugelradius r. Da die ganze Kugeloberfläche den Flächeninhalt 4πr2 besitzt, ist der volle Raumwinkel 4π. Der Raumwinkel wird mit der Einheit Steradiant (sr) angegeben.
\Omega = (\frac{A}{r^2}) \times \Omega_0
\Omega_0 = 1 \ sr
Vollwinkel: \Omega_{Kugel} = 4\pi \ sr
#
Winkelfunktionen im rechtwinkligen Dreieck
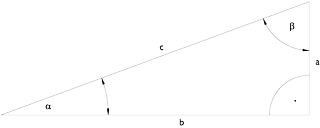
Sinus \ eines \ Winkel = \frac{GegenKathete}{Hypothenuse}\sin \alpha = \frac{a}{c}\sin \beta = \frac{b}{c}Consinus \ eines \ Winkel = \frac{Ankathete}{Hypothenuse}\cos \alpha = \frac{b}{c}\cos \beta = \frac{a}{c}Consinus \ eines \ Winkel = \frac{Ankathete}{Hypothenuse}\cos \alpha = \frac{b}{c}\cos \beta = \frac{a}{c}Tangens \ eines \ Winkel = \frac{GegenKathete}{Ankathete}\tan \alpha = \frac{a}{b}\tan \beta = \frac{b}{a}CoTangens \ eines \ Winkel = \frac{Ankathete}{GegenKathete}\tan \alpha = \frac{b}{a}\tan \beta = \frac{a}{b}
#
Satz des Pythagoras
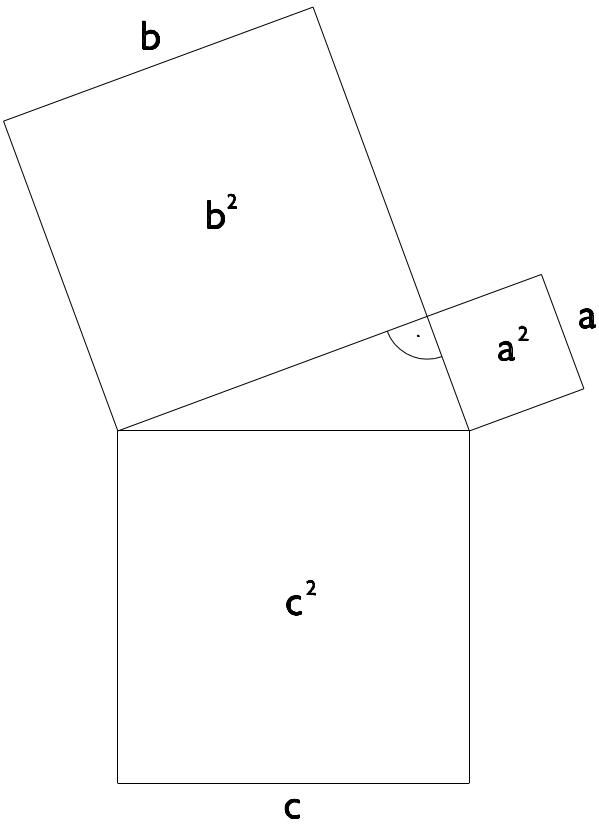
c^2 = a^2 + b {#2}c = \sqrt{a^2 + b^2}
#
Flächen
#
Quadrat
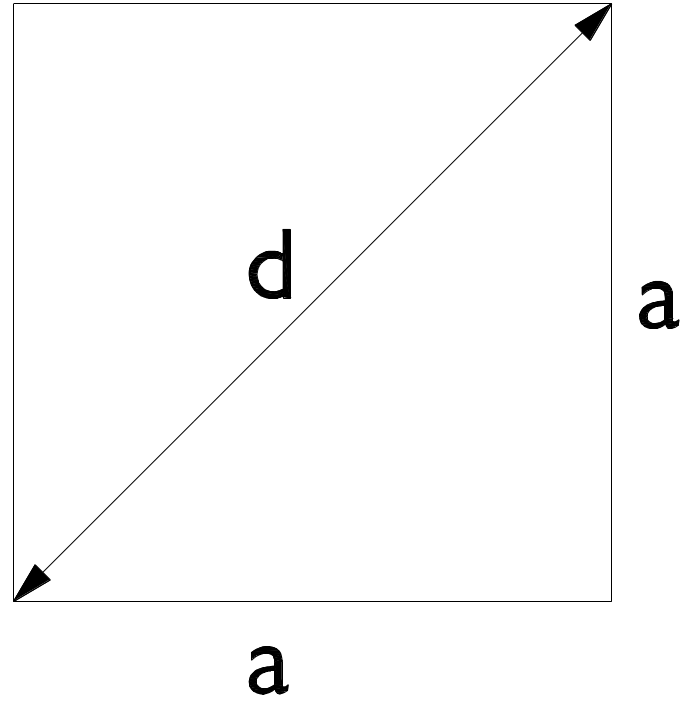
A = a {#2}a = \sqrt{A}d = a\sqrt{2}
#
Rechteck
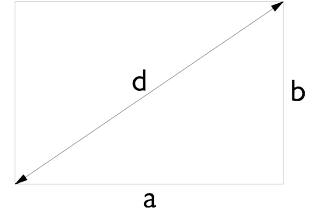
A = a \times b
d = \sqrt{a^2 + b^2}
#
Kreis
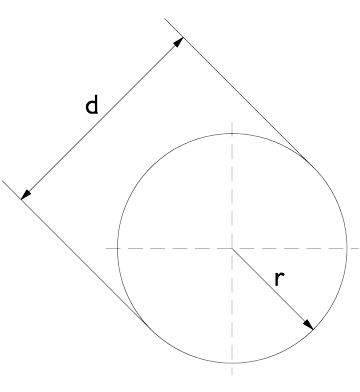
A = \frac{\pi}{4} \times d^2 = \boldsymbol{i} \pi \boldsymbol{i} r^2 \boldsymbol{i}U = 2 \times \boldsymbol{i} \pi \times r = \pi \times d \boldsymbol{i}
#
Kreisausschnitt
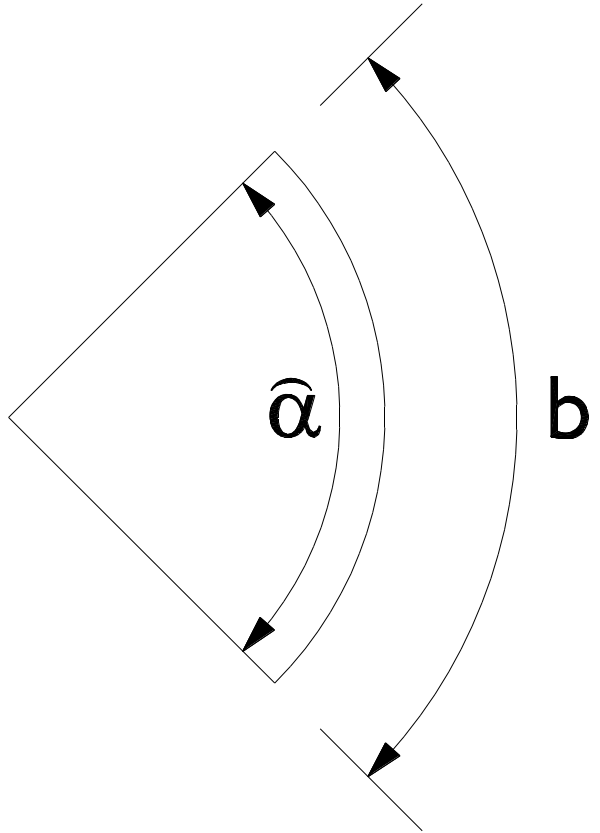
A = \frac{\pi}{360^\circ} \times r^2 \times \alpha = \frac{\bar{\alpha}}{2} \times r^2 = \frac{b \boldsymbol{i} r}{2}b = \frac{\pi}{180^\circ} \times r \times a \quad\quad \text{ Bogenlänge }\bar{\alpha} = \frac{\pi}{180^\circ} \times \alpha \quad\quad \bar{\alpha} = \text{ Winkel im Bogenmaß}\alpha = \frac{\pi}{180^\circ} \times \bar{\alpha} \quad\quad \alpha = \text{ Winkel im Gradmaß}
#
Körper
#
Würfel
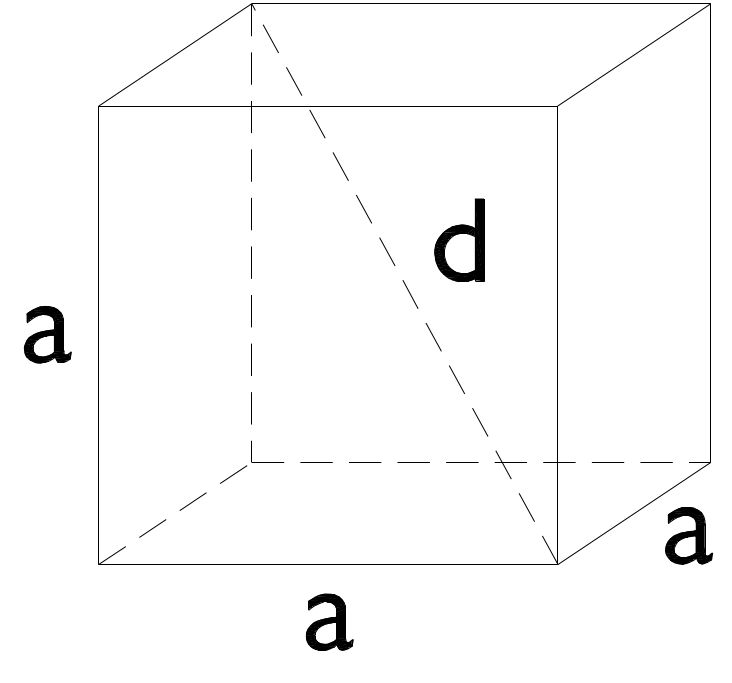
v=a {#3}A=6 \times a {#2}d=\sqrt{3} \times a
#
Quader
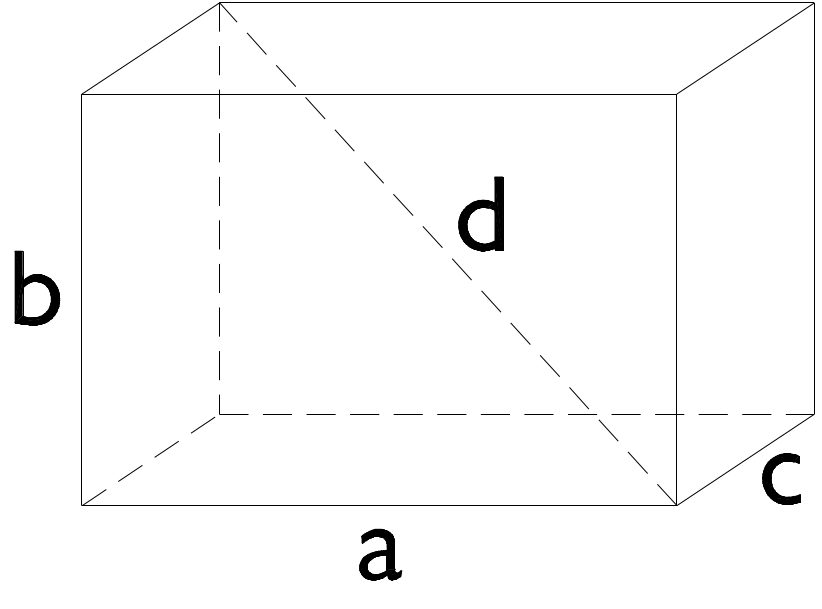
v=a \times b \times c
A=2(ab + ac + bc)
d= \sqrt{a^2 + b^2 + c^2}
#
Zylinder
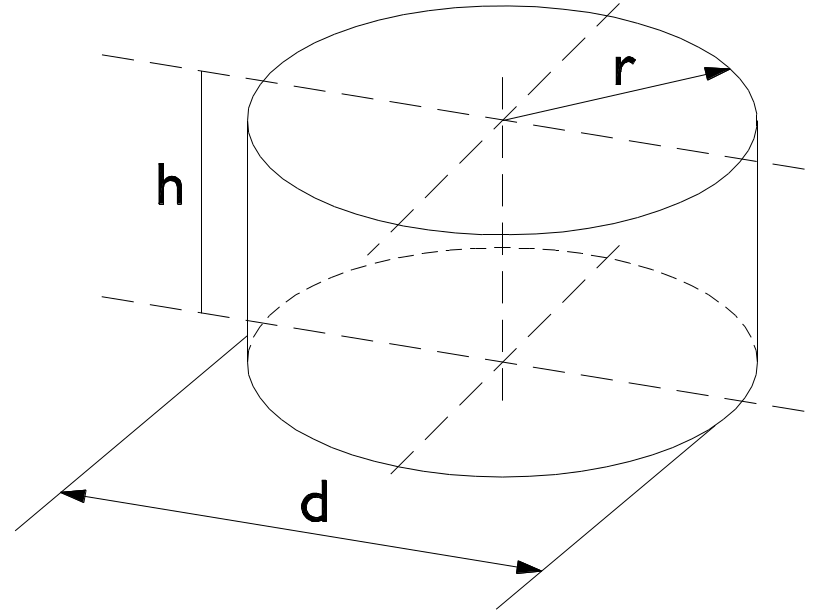
v= \frac{\pi}{4} \times d^2 \boldsymbol{i} hA= 2 \times \boldsymbol{i} \pi \times r \times h \boldsymbol{i}
#
Kugel
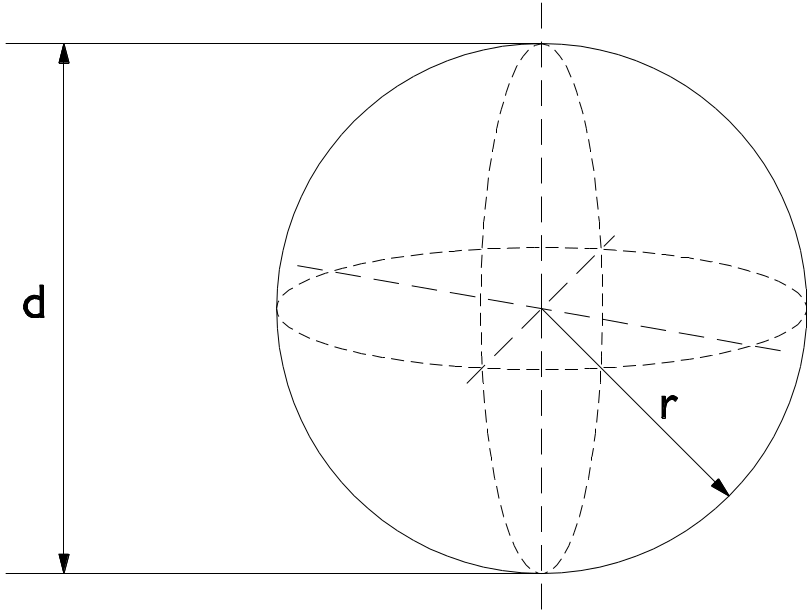
v= \frac{4}{3} \times \boldsymbol{i} \pi \times r^3 \boldsymbol{i}A= 4 \times \boldsymbol{i} \pi \times r^2 \boldsymbol{i}
#
Dezimal-, Hexadezimal- und Dualsystem
In der Computer- und Informationstechnologie werden zum Zählen und Rechnen neben dem Dezimalsystem ebenfalls das Hexadezimalsystem und das Dualsystem verwendet.
#
Dezimalsystem
Das Dezimalsystem (lat. Dezimus = „der Zehnte“) verwendet die Grundzahl (Basis) 10 zum Rechnen. Das Dezimalsystem ist heute das weltweit verbreitete Zahlensystem und stammt ursprünglich aus Indien. Seinen Ursprung hat es vermutlich durch den Umstand, dass der Mensch 10 Finger besitzt.
#
Hexadezimalsystem
Im Hexadezimalsystem werden Zahlen in einem Zahlensystem zur Basis 16 dargestellt. Das Hexadezimalsystem besteht aus 16 Ziffern, die mit den Zeichen 0 bis 9 und A bis F dargestellt werden. Im Gegensatz zum Dezimalsystem eignet sich das Hexadezimalsystem mit seiner Basis als vierte Zweierpotenz (16 = 24) zur einfacheren Beschreibung von Dualzahlen (Binärzahlen). So können achtstellige Binärzahlen als zweistellige Hexadezimalzahlen dargestellt werden (z. B. 10110011 = B3).
#
Dualsystem (Binärsystem)
Das Dualsystem (lat. Dualis = zwei enthaltend) wird auch als Binärsystem oder Zweiersystem bezeichnet und ist ein Zahlensystem mit der Basis 2, in dem nur zwei verschiedene Ziffern zur Darstellung von Zahlen verwendet werden. Wegen diesem Dualismus ist das Binärsystem Grundlage jeglicher digitalen Berechnung in Computern und Mikrochips. Dabei werden die Zahlen mit den Ziffern Null (0) und Eins (1) dargestellt.