#
Grundlagen der Fotometrie

#
Lichtstärke I
Die Lichtstärke (engl. Luminous oder Light Intensity) mit dem Formelzeichen I ist eine Basiseinheit des Internationalen Einheitensystems und wird in Candela (cd) gemessen.
Definition:
Ein Candela ist die Lichtstärke einer Strahlungsquelle, die in eine bestimmte Richtung monochromatisches Licht der Wellenlänge 555 nm mit der Strahlstärke 1/683 Watt pro Steradiant aussendet.
i=\frac{\Phi}{\Omega}Φ = Lichtstrom
Ω = durchstrahlter Raumwinkel
[ I ] = cd
Die Lichtstärke gibt die Lichtstromdichte (Intensität) einer Lichtquelle in eine bestimmte Richtung an, wobei die Lichtstärke bei verschiedenen Richtungen ungleichmäßig verteilt ist. Diese Richtungsabhängigkeit wird in Lichtstärkeverteilungskurven (LVK) angegeben, in denen die Lichtstärken für verschiedene Ausstrahlungswinkel dargestellt werden.
Die Lichtstärke beträgt i × cosα in Richtungen, die um den Winkel von der Flächennormalen geneigt sind. Bei einer diffus strahlenden, ebenen Fläche erhält man eine Lichtverteilungskurve, die wegen i × cosα ein Kreis darstellt. Eine solche strahlende Fläche bezeichnet man als Lambert-Strahler.
#
Lichtstrom Φ (phi)
Der Lichtstrom (engl. Luminous Flux) ist eine physiologische Messgröße und gibt die von einer Lichtquelle nach allen Seiten abgestrahlte und vom Auge bewertete Strahlungsleistung an. Strahlt eine Lichtquelle mit einer Lichtstärke I = 1 cd gleichmäßig in einem Raumwinkel = 1 sr, so strahlt sie einen Lichtstrom von = 1 lm aus. Die Einheit des Lichtstroms ist Lumen [lm].
\Phi = I \times \Omega \quad \quad \quad [Im = cd \times sr]
Die sichtbare Strahlungsleistung wird nicht in Watt angegeben, da das Auge für die Strahlung verschiedener Wellenlängen unterschiedlich empfindlich ist. Die Strahlungsleistung des Lichtstroms wird mit Hilfe des fotometrischen Strahlungsäquivalentes K(λ) ermittelt, das sich auf die V(λ)-Kurve der Hellempfindlichkeit des Auges bezieht. Der Maximalwert der fotometrischen Strahlungsäquivalenz Km liegt bei einer Wellenlänge von 555 nm und beträgt 683 Lumen/Watt. Ein Lichtstrom von 1 lm entspricht einer Leistung von 0,00144 W.
\phi = \imath K_m \int_{380nm}^{780nm} \phi _e{\lambda} \times V(\lambda) \times d\lambda \imath Φe = spektraler Strahlungsfluss = 683 lm
Φe bei λ (555 nm) = 1 W
Km = 683 lm/W
V(λ) bei 555nm = 1
#
Lichtstärkeverteilungskurven (LVK)
Der Lichtstrom Φ einer Lichtquelle strahlt nicht zu allen Seiten gleichmäßig ab. Die Lichtstärkeverteilung hängt dabei ganz stark von der Art und Bauform der Lichtquelle ab. Der Einbau der Lichtquelle in ein Gehäuse, eine Leuchte oder in ein optisches System verändert ebenfalls die Lichtstärkeverteilung der Lichtquelle. Durch eine entsprechende Konstruktion von Leuchten (Scheinwerfern) in Kombination mit einem passenden Leuchtmittel können für bestimmte Verwendungszwecke angepasste Lichtstärkeverteilungen erzielt werden. Eine Lichtstärkeverteilung wird in einem Polardiagramm eingezeichnet, wobei die Lichtquelle in der Mitte des Diagramms liegt und die Lichtstärke zum Rand des Diagramms abnimmt. Das Diagramm gibt die Lichtstärke Φ in Abhängigkeit von einem Abstrahlwinkel ε mit der Einheit Lumen an.
Es gibt verschiedene Kategorien von Lichtverteilungskurven. Dazu gehören um Beispiel:
- tiefstrahlend (nach unten strahlend)
- engstrahlend (enger Abstrahlwinkel)
- breitstrahlend (breiter Abstrahlwinkel)
- freistrahlend (großer Abstrahlwinkel)
- hochstrahlend (nach oben strahlend)
- tief-hochstrahlend (nach unten und nach oben strahlend)
- asymmetrisch oder schrägstrahlend
#
Lichtausbeute η (eta)
Das Lumen/Watt-Ratio wird auch als Lichtausbeute φ bezeichnet. Die Lichtausbeute gibt den erzeugten Lichtstrom im Verhältnis zu der aufgewendeten elektrischen Leistung an.
\eta = \frac{\phi}{P} \quad \quad \quad [Im/W]Lichtausbeuten verschiedener Lichtquellen:
Glühlampe 60 W η = 12 lm/W
Leuchtstofflampe 58 W η = 78 lm/W
Natriumdampf-Niederdrucklampe η = 105 lm/W
#
Leuchtdichte L
Die Leuchtdichte (engl. Luminance) ist ein Maß für den Helligkeitseindruck, den das Auge von einer selbstleuchtenden oder einer beleuchteten Fläche hat. Die Einheit der Leuchtdichte ist cd/m2. Ab Leuchtdichten von etwa 0,75 cd/m2 tritt eine Blendung des Auges ein.
L = \frac{I}{A} \quad \quad \quad [cd/m^2]I = Lichtstärke
A = gesehene Fläche
Steht die gesehene Fläche nicht senkrecht zum Beobachter, sondern um einen Winkel geneigt, so muss der Neigungswinkel bei der Berechnung der Leuchtdichte mit einbezogen werden.
A = A^* \times cos \alpha
A = gesehene Fläche
A* = tatsächliche Fläche
Für den Lambert-Strahler ist wegen der richtungsabhängigen Lichtstärke die Leuchtdichte L richtungsunabhängig.
Leuchtdichte einiger Lichtquellen:
Nachthimmel 0-7 cd/m2
Fluoreszenz bis 10-2 cd/m2
Mond 0,25 cd/m2
Grauer Himmel bis 0,3 cd/m2
Blauer Himmel bis 1 cd/m2
Kerzenflamme bis 1 cd/m2
Glühlampe, mattiert 5 - 40 cd/m2
Glühlampe, klar 200 - 3.000 cd//m2
Sonne am Horizont 600 cd/m2
Kohlelichtbogen bis 18.000 cd/m2
Mittagssonne bis 150.000 cd/m2
Xenon-Höchstdrucklampe 50.000 - 1.000.000 cd/m2
#
Reflektierte Leuchtdichte
Prinzipiell muss zwischen der Leuchtdichte eines Selbststrahlers und der Leuchtdichte einer reflektierenden Oberfläche unterschieden werden. Reflektierte Leuchtdichten können in folgende Gruppen eingeordnet werden und hängen entscheidend von Oberflächen ab:
Gerichtete Reflexion
Die reflektierte Leuchtdichte ist proportional zur einfallenden Leuchtdichte, der Eintrittswinkel ist gleich dem Austrittswinkel (z. B. Spiegel).Diffuse Reflexion
Die diffuse Reflektion ist ein Sonderfall, bei der ein Objekt in allen Richtungen die gleiche Leuchtdichte ausstrahlt (z. B. weiße Raufasertapete).Gemischte Reflexion
Die reflektierte Leuchtdichte setzt sich aus einem diffusen und einem gerichteten Anteil zusammen.
#
Beleuchtungsstärke E
Die Beleuchtungsstärke E (engl. Illuminance) ist ein Maß für das auf eine Fläche auftreffende Licht. Hierbei wird auch von der Lichtstromdichte gesprochen. Die Einheit der Beleuchtungsstärke ist Lux [lx].
E = \frac{\phi}{A} \quad \quad \quad \quad [Ix = Im/m^2]φ = Lichtstrom [ lm = cd × sr ]
A = beleuchtete Fläche
In den angelsächsischen Ländern wird die Beleuchtungsstärke vielfach in Foot Candle (fc) angegeben. Der Umrechnungsfaktor zwischen Lux und fc beträgt 10,76.
Lux/10,76 = fc
fx \times 10,76 = Lux
#
Fotometrisches Entfernungsgesetz
Die Beleuchtungsstärke nimmt mit dem Quadrat der Entfernung ab. Dieses gilt jedoch nur für punktartige Lichtquellen und senkrecht auftreffendes Licht. Das Entfernungsgesetz kann bei größeren Lichtquellen (z. B. Leuchtstoffröhren) erst verwendet werden, wenn die Entfernung der Lichtquelle 10-mal größer ist als der Lichtquellen-Durchmesser (r ≈ 10 × d).
E = \frac{\phi}{A} = \frac{I}{r^2}\phi = I \times \Omega
\Omega = \frac{A}{r^2}
#
Lamberts Cosinus-Gesetz
Trifft Licht aus einer Punktlichtquelle (Durchmesser der Lichtquelle klein gegenüber der Entfernung) unter einem Winkel α auf einen Punkt, muss das Cosinus-Gesetz angewendet werden.
Vertikal:
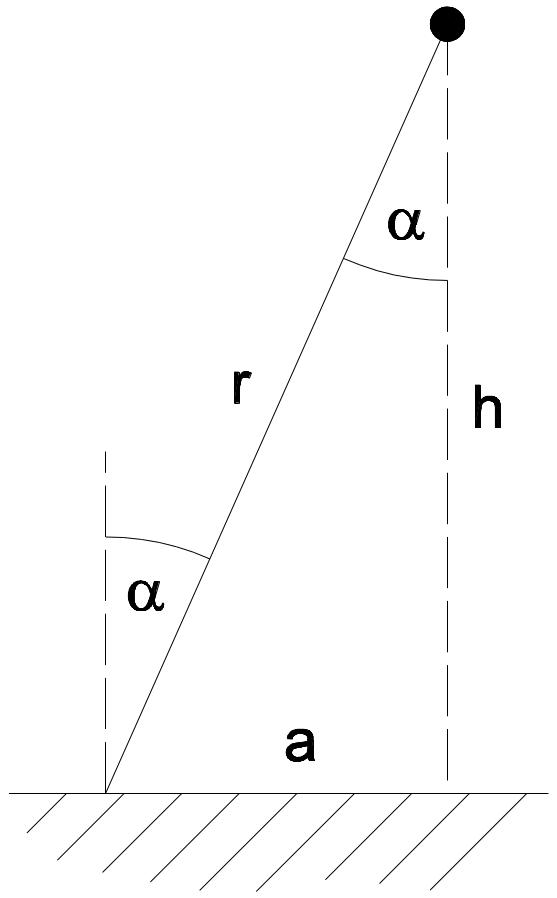
E = \frac{I}{r^2} \cos \alphaE = \frac{I}{h^2} (\cos \alpha) {#3}E = \frac{I \times h}{r^3} \cos\alpha = \frac{h}{r}
r^2 = a^2 + h^2
r = Radius
h = Höhe
a = horizontaler Abstand
Horizontal:
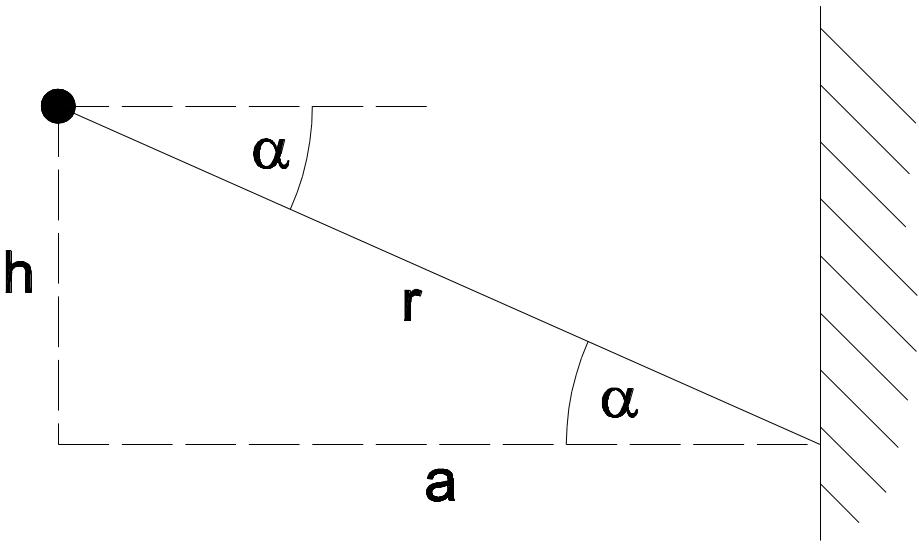
E = \frac{I}{r^2} \cos \alphaE = \frac{I}{a^2} (\cos \alpha) {#3}E = \frac{I \times a}{r^3} \cos\alpha = \frac{a}{r}
r^2 = a^2 + h^2
r = Radius
h = Höhe
a = horizontaler Abstand
#
Typische Beleuchtungsstärken
Notbeleuchtung ≈ 1 lx (vertikal in 0,2 m Höhe)
Flur ≈ 50 lx (vertikal)
Büro ≈ 500 lx (vertikal)
TV-Studio/Kamera ≈ 800 lx (horizontal)
Sonnenlicht im Sommer ≈ 100.000 lx
Sonnenlicht im Winter ≈ 10.000 lx
Bedeckter Himmel im Sommer ≈ 5.000 - 10.000 lx
Bedeckter Himmel im Winter ≈ 1.000 - 2.000 lx
Vollmond ≈ 0,2 lx
Mondlose Nacht ≈ 0,0003 lx
Grenze der Farbwahrnehmung ≈ 3 lx
Die Mindestbeleuchtungsstärken an Arbeitsplätzen werden in der DIN 5035, Teil 2 und in den entsprechenden Arbeitsstättenrichtlinien festgelegt.
#
Halbstreuwinkel
Der Halbstreuwinkel bezeichnet den Punkt in einem Lichtkegel, an dem die Beleuchtungsstärke auf 50 % der Beleuchtungsstärke vom Zentrum des Lichtkegels abgefallen ist. Der Halbstreuwinkel kann auch als Halbwertsbreite angegeben werden, die einem entsprechenden Lichtfelddurchmesser entspricht. Der Halbstreuwinkel ist wichtig beim Einleuchten von Flächen, die von mehreren Scheinwerfern beleuchtet werden. Eine optimale Ausleuchtung ist dann erreicht, wenn sich die Halbstreuwinkel der einzelnen Scheinwerfer genau berühren. Überlappen sich die Halbstreuwinkel, kommt es zu Lichtfeldern mit erhöhter Intensität, sind die Halbstreuwinkel zu weit auseinander, kommt es zu Schattenlöchern.
#
Gleichmäßigkeit der Beleuchtung
Die Gleichmäßigkeit einer Beleuchtung ist von der Art und Anordnung der eingesetzten Leuchtkörper, der Beleuchtungsgeometrie und der Art der angrenzenden Flächen abhängig. Eine homogene (gleichmäßige) Beleuchtung hat sowohl Auswirkungen auf den Sehkomfort als auch auf die Sehleistung. Bei inhomogenen Beleuchtungen entstehen Lichtinseln mit Schattenzonen, in denen ein geringer Kontrast zwischen Objekten und Umgebung herrscht. Die Helligkeitsunterschiede führen zu einer häufigen Adaptation des Auges, wodurch dieses schneller ermüdet. Die Gleichmäßigkeit der Beleuchtungsstärke kann durch zwei Kennzahlen bestimmt werden.
#
Gleichmäßigkeit der Leuchtdichte
Die örtliche Gleichmäßigkeit der Leuchtdichte wird aus den Leuchtdichtewerten Lmin (geringste Leuchtdichte im Bewertungsfeld), Lmax (maximale Leuchtdichte im Bewertungsfeld) und Lm (mittlere Leuchtdichte im Bewertungsfeld) gebildet. Es haben sich folgende Bewertungen die Gleichmäßigkeit der Leuchtdichten etabliert:
G_1 = \frac{L_{min}}{L_{max}}G_1 = \frac{L_{min}}{L_{m}}Lmin = geringste Leuchtdichte im gesamten Bewertungsfeld
Lmax = maximale Leuchtdichte im gesamten Bewertungsfeld
Lm = mittlere Leuchtdichte im gesamten Bewertungsfeld
In der DIN 5044 werden für die Längsgleichmäßigkeit GL und der Quergleichmäßigkeit GQ folgende Werte empfohlen:
| Stufe | Gleichmäßigkeit GL in Längsrichtung | Stufe | Gleichmäßigkeit GQ in Querrichtung | Bewertung | ||
|---|---|---|---|---|---|---|
| empfohlen | zulässig | empfohlen | zulässig | |||
| A | 1:1,3 | 1:1,6 | D | 1:2,5 | 1:4,0 | sehr gut |
| B | 1:1,6 | 1:2,0 | E | 1:4,0 | 1:6,0 | gut |
| C | 1:2,0 | 1:2,5 | F | 1:6,0 | 1:8,0 | befriedigend |
#
Gleichmäßigkeit der Beleuchtungsstärke
Die Gleichmäßigkeit der Beleuchtungsstärke wird aus der Beleuchtungsstärke Emin (geringste Beleuchtungsstärke im Bewertungsfeld), Emax (maximale Beleuchtungsstärke im Bewertungsfeld) und Em (mittlere Beleuchtungsstärke im Bewertungsfeld) gebildet.
G_1 = \frac{E_{min}}{E_{max}}G_1 = \frac{E_{min}}{E_{m}}Emin = geringste Beleuchtungsstärke im gesamten Bewertungsfeld
Emax = maximale Beleuchtungsstärke im gesamten Bewertungsfeld
Em = mittlere Beleuchtungsstärke im gesamten Bewertungsfeld