#
Grundlagen der Elektrotechnik

#
Formeltabelle
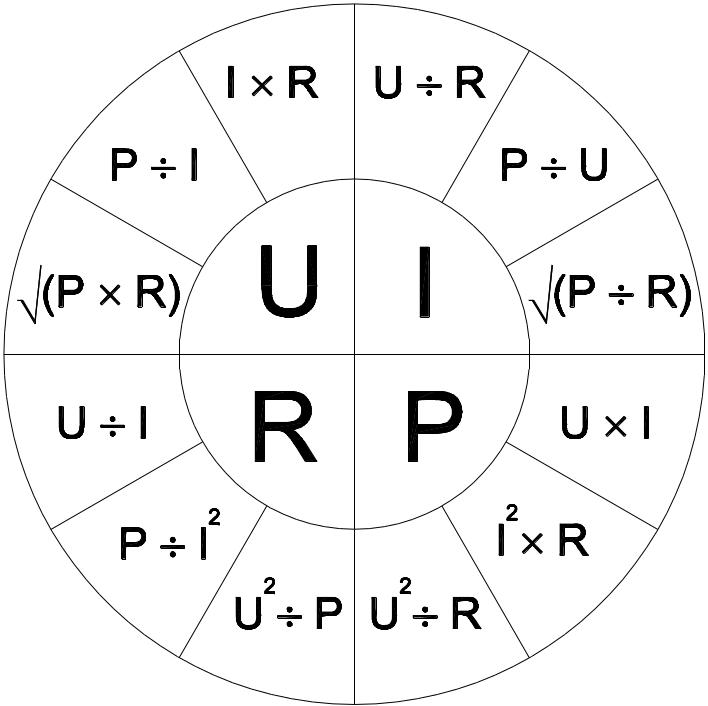
#
Elektrischer Strom [I]
Die Ursache eines elektrischen Stroms ist eine elektrische Spannung. Der elektrische Strom besteht dabei aus einer gerichteten Bewegung von elektrischen Ladungsträgern, den sog. Elektronen. Die elektrische Spannung dient dabei als „Motor“ der Elektronenbewegung. Aufgrund auftretender Magnetfelder bei der Elektronenbewegung wurde in den Anfangstagen der Elektrotechnik festgelegt, dass ein elektrischer Strom vom Pluspol zum Minuspol fließt. Tatsächlich bewegen sich jedoch die Elektronen vom Minuspol zum Pluspol. Die tatsächliche Stromrichtung der Elektronen (von – nach +) wird als physikalische Stromrichtung bezeichnet. In allen elektrischen Schaltungen wird jedoch mit der technischen Stromrichtung (von + nach –) gearbeitet. Die Stromstärke eines elektrischen Stroms gibt an, wie viele Ladungsträger (Elektronen) in einer bestimmten Zeit durch einen elektrischen Leiter fließen. Die elektrische Stromstärke ist eine Basisgröße des SI-Einheitensystems mit dem Formelzeichen I und der Einheit Ampere (A).
#
Elektrische Spannung [U]
Eine elektrische Spannung entsteht durch die Trennung von Ladungen, wobei diese getrennten Ladungen bestrebt sind, die Trennung wieder aufzuheben. Das Ausgleichsbestreben getrennter Ladungen wird als elektrische Spannung mit dem Formelzeichen U und der Einheit Volt (V) bezeichnet. Die Höhe einer elektrischen Spannung nennt man auch Potential, wobei damit vereinbarungsgemäß die Spannung eines Punktes zur elektrisch unbeeinflussten Erde (Erdpotential = 0 V) gemeint ist.
Grundsätzlich werden zwischen Gleichspannungen (DC = Direct Current) und Wechselspannungen (AC = Alternating Current) unterschieden. Eine Gleichspannung hat zu jedem Zeitpunkt den gleichen Wert mit derselben Polarität. Gleichspannungen werden z. B. durch Batterien oder Fotoelemente geliefert. Wechselspannungen werden mit Generatoren erzeugt, die eine Spannung mit wechselnder Polarität liefern.
#
Elektrischer (Ohm’scher) Widerstand [R]
Bei der Bewegung von Elektronen durch einen elektrischen Leiter strömen die Elektronen zwischen den Atomen eines elektrischen Leiters hindurch. Dabei stoßen sie gelegentlich mit den Atomen zusammen und verlieren so an Energie, wobei Wärme freigesetzt wird. Der Leiter setzt somit den Elektronen einen Widerstand entgegen. Es muss Arbeit aufgewendet werden, um einen konstanten Strom durch den Leiter aufrechtzuhalten.
Das Ohmsche Gesetz definiert den elektrischen Widerstand R (lat. resistantia) mit der Einheit Ohm [Ω]. Das Ohm’sche Gesetz ist eines der Grundgesetze der Elektrotechnik.
R = \frac{U}{I} \quad \quad [\Omega = \frac{V}{A}]G = \frac{1}{R} \quad \quad [S = \frac{V}{A}]
#
Elektrischer Widerstand von Leitern
R = \frac{\rho \times l}{A}R = \frac{1}{\kappa \times A}A = \frac{\pi \times d^2}{4}R = Widerstand [Ω]
Ρ (Roh) = Spezifischer Widerstand [(Ω × mm2)÷m]
κ (Kappa) = Spezifischer Leitwert [(S × m)÷mm2]
l = Leiterlänge [m]
A = Querschnittsfläche [mm2]
ρ von Kupfer bei 20° C = 0,0178 (Ω × mm2)÷m
κ von Kupfer bei 20° C = 56,18 (S × m)÷mm2
#
Elektrische Reihenschaltung
Der Strom an allen Verbrauchern (Widerständen) ist gleich groß, die Spannung teilt sich auf.
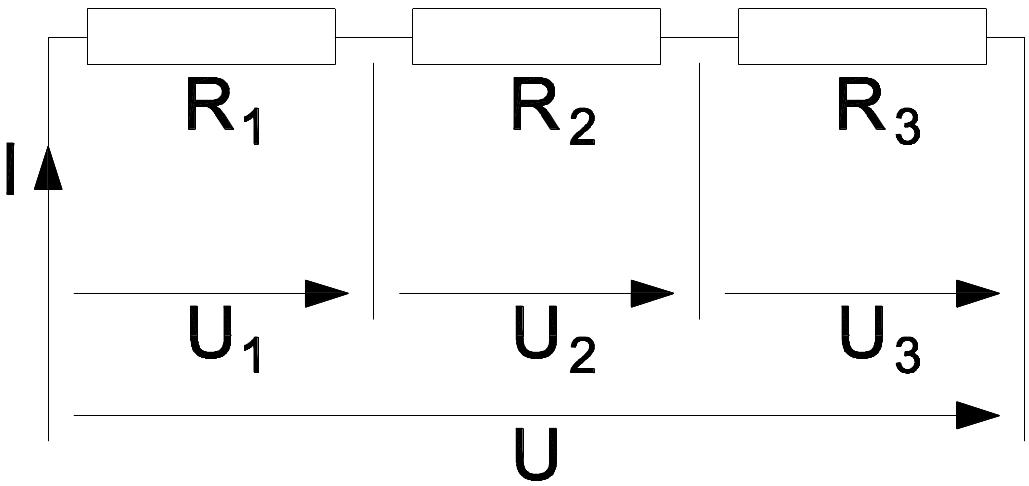
R = R_1 + R_2 + R_3 + ... \quad \quad \quad \text{(Gesamtwiderstand)}U = U_1 + U_2 + U_3 + ... \quad \quad \quad \text{(Gesamtspannung)}U = I \times R
U_n = I \times R_n
#
Elektrische Parallelschaltung
Die Spannung an allen Verbrauchern (Widerständen) ist gleich groß, der Strom teilt sich auf.
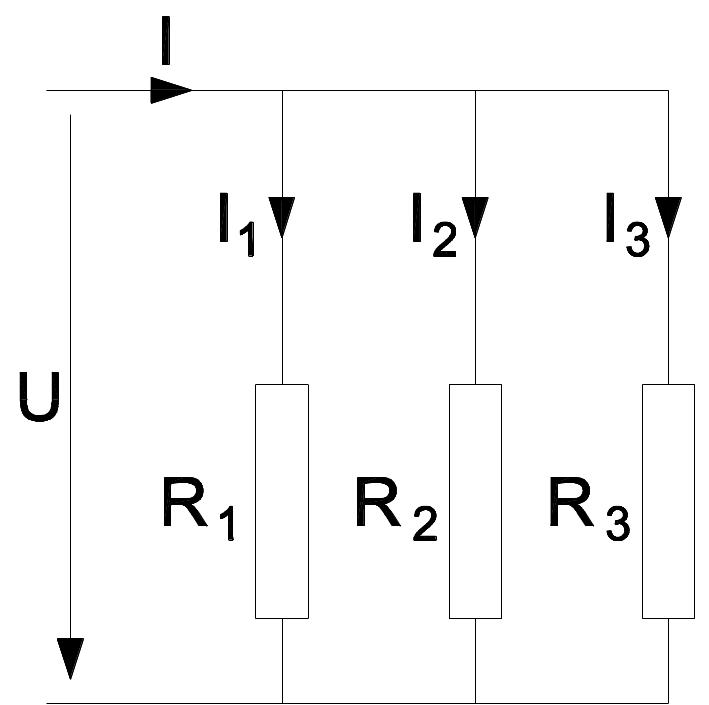
R = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ... \quad \quad \quad \text{(Gesamtwiderstand)}I = I_1 + I_2 + I_3 + ... \quad \quad \quad \text{(Gesamtstrom)}I = \frac{U}{R}I_n = \frac{U}{R_n}
#
Elektrische Leistung (P)
Die Leistung gibt die Arbeit an, die in einer bestimmten Zeit verrichtet wird. Die elektrische Leistung P ist das Produkt aus Spannung und Strom mit der Einheit Watt [W]
P = U \times I \quad \quad \quad \quad [ W = V \times A ]
P = I^2 \times R \quad \quad \quad \quad[ W = A^2 \times \frac{V}{A} ]P = \frac{U^2}{R} \quad \quad \quad \quad[ W = V^2/V/A ]Die Leistungsformel ist neben dem Ohm’schen Gesetz eine der wichtigsten Formeln in der Elektrotechnik.
#
Elektrische Arbeit (W)
Die elektrische Arbeit (W) ist das Produkt aus elektrischer Leistung und der Zeit t in Sekunden mit der Einheit [Ws (Watt-Sekunden)] oder [kWh (Kilowatt-Stunden)]
W = U \times I \times t \quad \quad \quad [ Ws = V \times A \times s ]
W = P \times t
1 kWh = 3,6 \times 10^6 Ws
1 Nm = 1 Ws = 1 J
#
Kosten elektrischer Arbeit (K)
Kosten = Arbeit \times tariflicher Preis
K = W \times T \quad \quad \quad [ K = kWh \times €/kWh ]
K = P \times t \times T
#
Wirkungsgrad (η)
Der Wirkungsgrad η ist der Quotient aus der abgegebenen Arbeit Wab (Leistung Pab) zu der zugeführten Arbeit Wzu (Leistung Pzu). Die Verlustarbeit oder –leistung ist die Differenz zwischen der abgegebenen Arbeit (Leistung) und aufgenommenen Arbeit (Leistung). Der Gesamtwirkungsgrad in einem System ist das Produkt der Einzelwirkungsgrade.
\eta = \frac{W_{ab}}{W_{zu}}\eta = \frac{P_{ab}}{P_{zu}}\eta_{gesamt} = \eta_1 \times \eta_2 \times .... \times \eta_nDa meistens der Wirkungsgrad in Prozent ausgedrückt wird, muss der Quotient mit 100 % multipliziert werden.
#
Wechselspannung und -strom
Der Spannungs- und Strompegel einer Gleichspannung (Gleichstrom) ist immer gleich. Wechselspannungen und -ströme hingegen haben einen sinusförmigen Verlauf mit einem Nulldurchgang, einer positiven und einer negativen Halbwelle. Diese Eigenschaft ermöglicht zum Beispiel eine beliebige Transformierbarkeit der Spannung für den Ferntransport elektrischer Energie. Beim Betrieb von Wechselspannungen und -strömen ergeben sich einige Besonderheiten, die sich teils vorteilhaft, aber auch teils störend auswirken können.
#
Induktiver Widerstand
Werden Transformatoren oder Drahtspulen jeglicher Art von einem Wechselstrom durchflossen, entsteht der sog. induktive Widerstand. Der induktive Widerstand ergibt sich durch die physikalische Eigenschaft der magnetischen Induktion und wird umso größer, je höher die Frequenz des Wechselstroms ist. Der Scheinwiderstand (Z) ist die Summe des induktiven (XL) und des ohmschen (R) Widerstands.
X_L = 2\pi \times f \times L
L = Induktivität
f = Frequenz (Kreisfrequenz: ω = 2π × f)
#
Kapazitiver Widerstand
Kapazitäten wie Kondensatoren sind für Gleichströme vollkommen undurchlässig (unendlicher Widerstand). Nur Wechselströme werden von Kapazitäten durchgelassen. Die Leitfähigkeit einer Kapazität hängt von ihrer Größe und der Frequenz des Wechselstroms ab. Je größer die Frequenz, desto geringer der Widerstand der Kapazität. Der kapazitive Widerstand verhält sich genau entgegengesetzt zum induktiven Widerstand. Der Scheinwiderstand (Z) ist die Summe des kapazitiven (XC) und ohmschen (R) Widerstands.
X_C = \frac{1}{2\pi \times f \times C}C = Kapazität
f = Frequenz (Kreisfrequenz: ω = 2π × f)
Phasenverschiebung und Leistung
Induktivitäten und Kapazitäten erzeugen in der Wechselstromtechnik eine Phasenverschiebung zwischen der Spannung und dem Strom. Bei Induktivitäten verzögert sich der Strom gegenüber der Spannung um 90°, bei Kapazitäten eilt der Strom gegenüber der Spannung um 90° voraus. Diese Phasenverschiebung hat für die erzeugbare elektrische Wirkleistung (P) eine wichtige Bedeutung. Die Wirkleistung ist immer dann am größten, wenn Spannung und Strom in Phase sind (0°). Tritt eine Phasenverschiebung zwischen Spannung und Strom auf, wird eine Blindleistung (Q) erzeugt, die praktisch nicht nutzbar ist und als Ballast nur die Leitungswege in Anspruch nimmt. Diese Blindleistung wird im ersten Moment vom Verbraucher aufgenommen, dann allerdings sofort an die Quelle zurückgegeben. Die Blindleistung pendelt so nutzlos zwischen Verbraucher und Stromquelle hin und her. Bei einer maximalen Phasenverschiebung von 90° wird nur noch Blindleistung übertragen, so dass die Wirkleistung auf null zurückgeht.
Die durch Phasenverschiebung erzeugte Blindleistung macht sich im Stromversorgungsnetz überall bemerkbar, wo Induktivitäten (z. B. Trafos und Generatoren) oder Kapazitäten (z. B. lange Kabelwege) vorhanden sind. Dies kann zu einer Verringerung der abgreifbaren Wirkleistung führen, im Extremfall sogar soweit, dass keine Wirkleistung übertragen wird. Die entstehende Blindleistung muss vom Stromerzeuger ohne weiteren Nutzen erzeugt werden. Ebenso muss das gesamte elektrische Netz um den Faktor der auftretenden Blindleistung größer dimensioniert werden. Aus diesen Gründen streben die Netzbetreiber in ihren Netzen eine möglichst geringe Blindleistung an. Stromgroßabnehmer wie z. B. Theater sind deswegen verpflichtet, den maximalen Phasenverschiebungswinkel möglichst gering zu halten. Um dies zu erreichen, können zur Kompensation entsprechend angepasste Induktivitäten und Kapazitäten auf der Seite des Blindleistungserzeugers eingefügt werden. Durch die Blindleistungs-kompensatoren werden Phasenverschiebungen bereits am Verbraucher ausgeglichen und so das elektrische Netz nicht mit unnötigen Blindleistungen belastet.
#
Blindleistung, Scheinleistung und Cos φ
Die Wirkleistung (P) und Blindleistung (Q) ergeben zusammen die Scheinleistung (S) eines Gerätes oder einer Leitung im Wechselstromkreis. Die Scheinleistung ist die effektiv nutzbare elektrische Energie am Verbraucher. Wegen der auftretenden Blindleistung ist die Scheinleistung um den Phasenverschiebungswinkel φ (Phi) zur Wirkleistung verschoben.
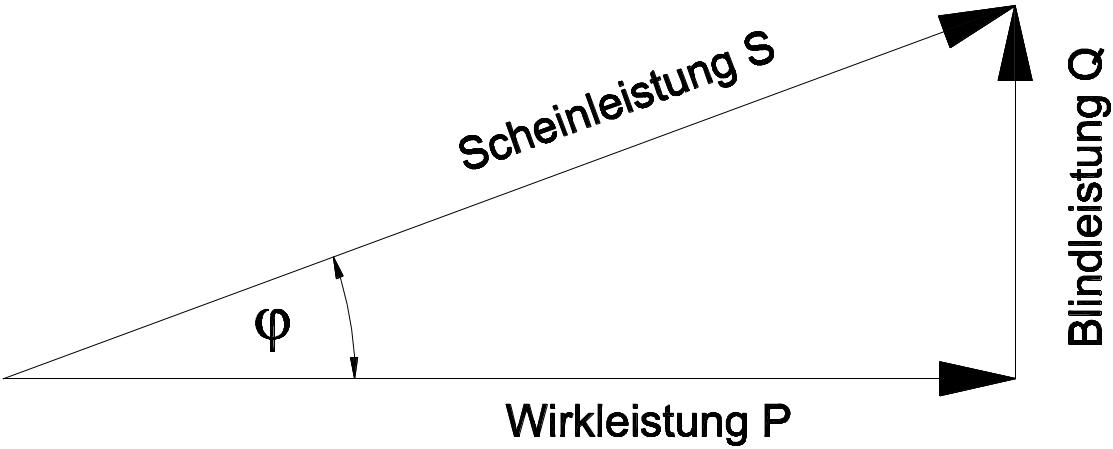
S^2 = P^2 + Q {#2}P = U \times I \times cos \phi
P2 = S^2 - Q {#2}Q = U \times I \times sin \phi
Q^2 = S^2 - P {#2}cos \phi \leq 1
S = Scheinleistung [VA]
P = Wirkleistung [W]
Q = Blindleistung [var]
φ = Phasenverschiebungswinkel
cos φ = Leistungsfaktor
Die Blindleistung wird durch eine Verringerung des Phasenverschiebungswinkels φ vermindert. Üblichweise entstehen Blindleistungen durch Induktivitäten (+ 90° Phasenverschiebung) wie z. B. Vorschaltgeräte oder Transformatoren. Zur Blindleistungskompensation werden angepasste Kapazitäten (Kondensatoren, - 90° Phasenverschiebung) eingesetzt, die den von Induktivitäten erzeugten Phasenverschiebungswinkel kompensieren und im Idealfall die Blindleistung ganz aufheben.
#
Cos φ bei Aggregaten
Wegen dem Phasenverschiebungswinkel φ werden Leistungsangaben für mobile Aggregate zur Stromversorgung von Freilichtbühnen o. ä. grundsätzlich in der Scheinleistung S (üblicherweise mit der Einheit KVA) angegeben. In der Regel kann mit einem Leistungsfaktor (cos φ) von 0,8 gerechnet werden.
S = \frac{P}{cos\phi}S = Scheinleistung [VA] (Aggregatgröße)
P = Wirkleistung [W] (Verbraucherleistung)
φ = Phasenverschiebungswinkel
cos φ = Leistungsfaktor ≈ 0,8
Um eine Überlastung des Aggregates zu vermeiden, sollte zusätzlich ein Sicherheitsfaktor eingerechnet werden. Bei normalen Anwendungen ist ein Sicherheitsfaktor von 0,8 ausreichend. Werden jedoch Dimmersysteme an ein Aggregat angeschlossen, sollte wegen der hohen induktiven Lasten (Blindleistungen) mit einem Sicherheitsfaktor von ca. 0,65 gerechnet werden.
P = S \times cos \phi \times Sicherheitsfaktor
#
Gleichzeitigkeitsfaktor
Mit dem Gleichzeitigkeitsfaktor g wird die Tatsache berücksichtigt, dass in einer elektrischen Anlage nie alle Geräte gleichzeitig mit voller Last betrieben werden. Der Gleichzeitigkeitsfaktor ist eine wichtige Kenngröße zur Dimensionierung elektrischer Anlagen. Dabei stützt sich der Gleichzeitigkeitsfaktor in der Regel auf Erfahrungen und kann deshalb immer nur als Richtwert gelten.
Für die Dimensionierung einer elektrischen Anlage ist die Kenntnis aller anzuschließender Anlagenteile und ihren Anschlussleistungen notwendig. Jedem Objekt (Gebäude, Bühne, Veranstaltungssaal, etc.) liegen unterschiedliche Nutzerforderungen, baurechtliche Auflagen, technische Einrichtungen und haustechnische Anlagen zugrunde. Eine Erhebung der einzelnen Anschlusswerte ist dabei unerlässlich, um die Dimensionierung der Gesamtanlage bestimmen zu können.
In der Veranstaltungstechnik spielt der Gleichzeitigkeitsfaktor eine untergeordnete Rolle, da anders als in der Gebäude- oder Anlagentechnik eher davon ausgegangen werden sollte, dass alle angeschlossenen Geräte mit voller Leistung betrieben werden.
#
Drehstrom
In einem Dreiphasenwechselstromsystem werden um einen rotierenden Magneten drei Spulen um 120° versetzt angeordnet. Durch die Rotation des Magneten wird in jeder Spule eine Wechselspannung induziert. Durch die versetzte Anordnung der Spulen haben die drei Ausgangsspannungen einem Phasenverschiebungswinkel von 120°. Jede Spule wird als Strang bezeichnet, so dass die erzeugten Spannungen auch Strangspannungen genannt werden. Durch Verkettung der Strangenden entsteht entweder die Sternschaltung oder die Dreieckschaltung. Die Dreieckschaltung findet jedoch nur selten Verwendung.
Die Sternschaltung ermöglicht den Aufbau eines Vierleiternetzes mit den drei Außenleitern L1 bis L3 und einem Mittelleiter N. Zwischen den Außenleitern beträgt die Spannung UA = 400 V, zwischen den Außenleitern und dem Mittelleiter UL1/L2/L3 = 230 V. Durch das Vierleiternetz ergeben sich verschiedene Anschlussmöglichkeiten für Verbraucher (dreiphasiger und zweiphasiger Anschluss mit 400 V zwischen den Außenleitern sowie einphasiger Anschluss mit 230 V zwischen den Außenleitern und dem Neutralleiter).
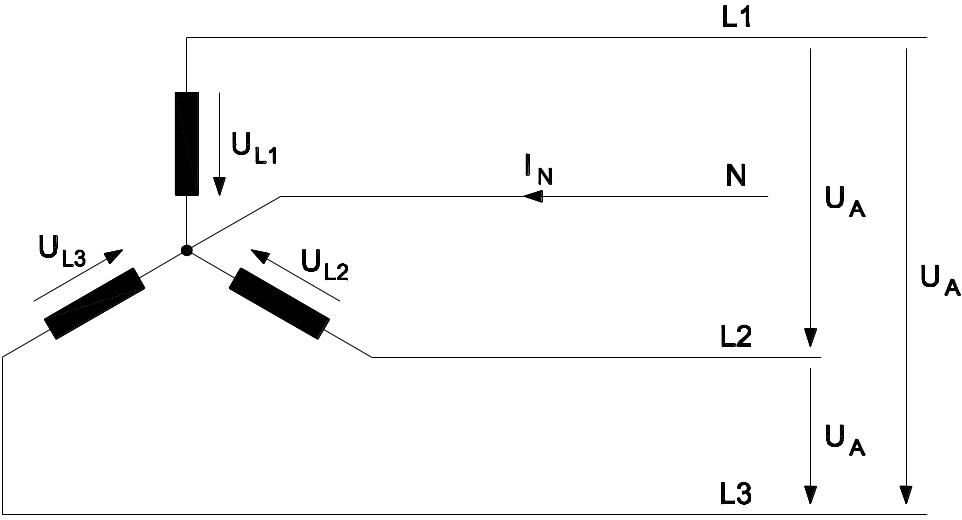
U_{L1/L2/L3} = 230 VU_A = 400 V
U_{L1/L2/L3} = \frac{U_A}{\sqrt3}I_N = 0 \quad \quad \quad \quad (bei Symmetrie)
S = \sqrt3 \times U_A \times I_N
P = \sqrt3 \times U_A \times I_N \times cos \phi
Q = \sqrt3 \times U_A \times I_N \times sin \phi
Bei gleichmäßiger, symmetrischer Belastung der drei Außenleiter bleibt der Mittelleiter stromlos. Bei ungleichmäßiger Belastung der Außenleiter fließt ein Teilstrom über den Mittelleiter zurück. Im Idealfall ist immer darauf zu achten, dass alle drei Phasen gleichmäßig belastet werden.
Beim Anschluss von Verbrauchern an mobile Aggregate zur Stromerzeugung ist unbedingt auf symmetrische Belastung der Außenleiter zu achten. Eine unsymmetrische Belastung kann im schlimmsten Fall durch ungleichmäßige Lastaufteilung zur Zerstörung des Aggregates führen. Ebenso ist der Leistungsfaktor bei der Dimensionierung des Aggregates zu berücksichtigen.