#
Farbe und farbmetrik

#
Farbe
Mit den drei Typen der Netzhautrezeptoren können insgesamt ungefähr 7 Millionen Farben (auch als Farbvalenzen bezeichnet) wahrgenommen werden. Das Auge arbeitet dabei integrierend, d. h., im Gegensatz zum Ohr können die einzelnen Anteile einer Lichtstrahlung nicht wahrgenommen werden. Alle spektralen Anteile einer Lichtstrahlung werden in ihrer Gesamtheit als Farbreiz von der Netzhaut erfasst und vom Gehirn als Farbe verarbeitet. Dabei können auch Farben entstehen, die im Spektrum der Lichtstrahlung nicht vorkommen, wie die Purpurtöne zwischen Rot und Blau. Verschiedene Farbreize können dabei den gleichen Farbeindruck hervorrufen (Metamerie). Die Farbempfindung wird von verschiedenen Faktoren beeinflusst: Art der Lichtquelle, individuelles Farbempfinden, Objektgröße und Objekthintergrund sowie Betrachtungswinkel und Betrachtungsposition.
Unbunte Farben (achromatische Farben) umfassen alle grauen Farben sowie Schwarz und Weiß. Das Auge kann dabei, abhängig von den Bedingungen, zwischen 50 und 100 Grautöne unterscheiden.
Die Kategorie der bunten Farben (chromatische Farben) umfasst alle anderen Farben. Bei gleicher Helligkeit und Buntheit können etwa 120 verschiedene Farbtöne vom Auge unterschieden werden.
Körperfarben sind die Oberflächenfarben von Objekten und lassen sich durch Farbton, Sättigung und Dunkelstufe (Helligkeit) charakterisieren. Die Farbreizfunktion (spektrale Verteilung) der Körperfarben (Sekundärstrahler) wird bestimmt durch die Oberflächeneigenschaften des Materials und der Beleuchtung. Körperfarben entstehen durch die Reflektion und Absorption bestimmter Wellenlängen der einfallenden Lichtstrahlen.
Selbstleuchter sind Lichtquellen jeglicher Art, die durch Farbton, Sättigung und Helligkeit charakterisiert werden. Bei Selbstleuchtern (Primärstrahlern) ist die Farbreizfunktion (spektrale Verteilung) identisch mit der spektralen Verteilung der Lichtquelle.
Der Farbton (Buntton) ist das am stärksten ausgeprägte Farbmerkmal und kennzeichnet die Art der Buntheit einer Farbe (Blau, Grün, Gelb, usw.). Qualitativ lassen sich Farbtöne in so genannten Farbkreisen darstellen. Ein Farbton ist eine einzige Wellenlänge aus dem Spektrum des Sonnenlichts (monochromatisches Licht) und stellt die reinste nur mögliche Farbe dar, wobei die Farbe zu 100 % gesättigt ist.
Die Sättigung (Buntheit) gibt den Anteil von Weiß oder Schwarz (Unbuntfarben) in einer reinen Farbe an. Der Anteil der Unbuntfarben bestimmt, ob eine Farbe kräftig oder verblasst ist. Sehr stark entsättigte Farben werden Pastellfarben genannt.
Die Helligkeit gibt die Stärke der Lichtempfindung an und wird bei Oberflächenfarben auch als Dunkelstufe bezeichnet.
Die Farbart (Buntart) ist eine Kombination aus dem Farbton und der Sättigung. Die Sättigung wird dabei durch den Weiß- bzw. Schwarzanteil der Farbe bestimmt.
Der Buntgrad gibt das Ausmaß des Buntseins bei Mischfarben wieder. Je größer der Buntgrad, desto intensiver ist die bunte Farbe. Jede Farbnuance einer Mischfarbe besteht aus einem Buntwert (Farbwert) und einem Unbuntwert (Grauwert), wobei der Buntwert aus bunten Grundfarben und der Unbuntwert aus bunten und unbunten Grundfarben gebildet werden kann.
Die Farberklärungen sind in der DIN 5033 Teil 1 näher definiert.
#
Farbempfindung
Farben rufen beim Beobachter eine ganz bestimmte Wirkung hervor. So kann zwischen kalten und warmen Farben unterschieden werden, zwischen Freude und Leid oder Schönes und Hässliches. Bei all diesen Wirkungen spielen Emotionen, individuelle Stimmungsbewertung, situationsbedingte und symbolisierte Assoziationen sowie die persönliche Beziehung zu einer Farbe eine große Rolle.
Warme Farben: Die Wärmezuordnung erfolgt durch die Assoziation von Sonne und Feuer. Warme Farben enthalten die Farbe Gelb. Beispiele sind Gelborange, Rot oder Gelbgrün.
Kalte Farben: Kalte Farben enthalten die Farbe Blau. Hier spielt die Assoziation zu Eis und tiefblauen Seen eine Rolle. Beispiele sind Grünblau, Blau, Violett. Die Farbe Grün kann eine kalte wie auch eine warme Farbe sein, tendiert jedoch eher zu den kalten Farben. Grün kann eine vermittelnde Rolle spielen.
Pastellfarben: Mit Weiß oder Grau gemischte Farben eignen sich für eine zarte und kultivierte Wirkung. Pastellfarben vermitteln häufig eine vornehme und dezente Stimmung.
Hochgesättigte Farben: Farben mit einem reinen Buntgrad, also ohne Anteile von Weiß oder Schwarz, bewirken einen kräftigen, aggressiven Eindruck. Sie können Kraft und Macht vermitteln sowie positive wie negative Stimmungen hervorrufen.
#
Bedeutung von Farben:
#
Farbmetrik
Die Farbmetrik ist die Lehre von den Maßbeziehungen zwischen den Farben. Sie beschreibt, unter welchen Umständen zwei Farbreize für das Auge gleich aussehen. Die Farbe wird ausschließlich als Farbempfindung, also Sinnesempfindung, aufgefasst. Dabei wird zwischen Farbvalenzmetrik (niedere Farbmetrik) und Farbempfindungsmetrik (hohe Farbmetrik) unterschieden.
#
Farbvalenzmetrik
In der Farbvalenzmetrik werden durch physikalische Reize hervorgerufene Farbempfindungen gemessen. Die psychologische Seite der Farbwahrnehmung (Farbinterpretation) wird dabei nicht mitberücksichtigt.
#
Farbempfindungsmetrik
In der Farbempfindungsmetrik werden die Empfindungsunterschiede und Harmonien für Farben untersucht und in Relation zu den physikalischen Reizen gestellt. Insbesondere werden Farbdifferenzen, Farbschwellen und Farbanordnungen untersucht.
#
Historische Entwicklung der Farbenlehre
#
Isaac Newton (1643-1727)
Als erster Forscher machte Isaac Newton systematische Experimente mit den Farben des Lichtspektrums. Er konnte nachweisen, dass sich weißes Licht mit Hilfe eines Prismas in seine Spektralfarben zerlegen lässt. Die Kanten eines Prismas brechen einfallende Lichtstrahlen in Abhängigkeit ihrer Wellenlänge verschieden stark, was einen Regenbogeneffekt zur Folge hat. Newton hat sieben Farben erkannt, aus denen er einen Farbenkreis konstruierte. Die drei deutlichsten Farben, Rot, Grün und Violett, waren für Newton die Grundfarben der Physik. Newton war der Auffassung, dass Licht eine Korpuskularstrahlung (Teilchenstrahlung) ist.
#
Johann Wolfgang von Goethe (1749-1832)
Im Gegensatz zu Newton betrachtete Goethe einen schwarzen Streifen vor einem weißen Hintergrund durch ein Prisma. Dabei sah er das sog. Kantenspektrum, bestehend aus den Farben Gelb, Blau und Purpur, die Goethe als Primärfarben festlegte. Daraus entwickelte er einen Farbenkreis, in dem sich die drei Primärfarben Gelb, Blau und Purpur mit den von Goethe definierten Sekundärfarben Orange, Violett und Grün abwechseln. Dieser Farbenkreis zeigt die jeweiligen Komplementärfarben, die von Goethe als harmonisch interpretiert wurden. Der Farbkreis Gelb-Orange-Purpur-Violett-Blau-Grün setzte sich in der Folge wegen seiner Regelmäßigkeit in der künstlerischen Lehre durch, wobei Gelb, Purpur und Blau die drei subtraktiven Grundfarben des modernen Farbdrucks vorwegnehmen.
#
Thomas Young (1773-1829)
Thomas Young verhalf der Wellentheorie des Lichts zum Durchbruch. Sein wichtigster Beitrag jedoch war seine Theorie der Trichromazität des Auges, also der Existenz dreier Elemente im Auge, die für unterschiedliche Wellenlängen des Lichts empfindlich sind. Als die drei Grundfarben schlug er Rot, Gelb und Blau vor, korrigierte aber später seine Aussage zu Rot, Grün und Blau.
#
Philipp Otto Runge (1777-1810)
Trotz Kritik an Goethes Farbenlehre beinhaltet die zeitgleich von Runge festgelegte Farbenlehre wesentliche Grundsätze Goethes, die er fast mit denselben Worten wie Goethe beschreibt. Diese Grundsätze haben auch heute noch ihre Gültigkeit. Runge definierte ein Farbordnungssystem in Kugelform, bei dem Goethes Farbenkreis den Äquator der Kugel bildet. Vom Äquator ausgehend fügte er die beiden Pole „Weiß“ oben und „Schwarz“ unten hinzu. Mit diesem Aufbau lässt sich die Mischung einer Buntfarbe mit Schwarz oder Weiß darstellen, jedoch nicht die für unsere Empfindung andersartige Intensitätsveränderung durch Aufhellung mit Licht oder Verdunkelung mit Finsternis. Aus diesem Grund nahm Runge an, dass Farben in einer doppelten Art, d. h. durchsichtig und undurchsichtig, vorkommen. Für Runge als Maler hatte diese Farbenlehre den Charakter einer Weltanschauung, die auf Idealfarben basiert.
#
Hermann Günter Grassmann (1809-1877)
Der deutsche Mathematiker Grassmann formulierte 1853, neben anderen Errungenschaften, die drei Gesetze der additiven Farbmischung, die seitdem ihre Gültigkeit besitzen:
- Für das Ergebnis einer additiven Mischung ist nur das Aussehen, nicht die spektrale Zusammensetzung der Einzelkomponenten maßgebend
- Alle Farbmischungen verlaufen stetig
- Zum Festlegen einer Farbe sind drei Bestimmungsstücke (Farbvalenzen) notwendig und hinreichend
#
James Clark Maxwell (1831-1879)
James Clark Maxwell gilt als Begründer der elektromagnetischen Theorie des Lichts. Mit seiner spektakulären Dreifarbenprojektion bewies er 1861, dass alle Farben durch die drei Grundfarben Rot, Grün und Blau synthetisiert werden können. Zudem führte er als Erster Messungen von Spektralwertkurven durch.
#
Hermann von Helmholtz (1821-1894)
Der deutsche Physiologe Hermann von Helmholtz führte die Messungen von Maxwell fort und verfeinerte sie. Zur Erklärung der Messkurven und der Gesetze der Farbmischung griff Helmholtz die Idee von Young auf, indem er drei Typen von Sinneszellen in der Netzhaut mit unterschiedlichen spektralen Empfindlichkeiten für das Farbensehen verantwortlich machte. Diese Theorie des Farbensehens von Young und Helmholtz, auch „Dreikomponenten-Theorie“ genannt, ist heute experimentell gut gesichert.
#
Edwald Hering (1834-1881)
Der österreichische Physiologe Hering greift die vorhergehenden Theorien von Young und Helmholtz kräftig an und formuliert seine „Gegenfarben-Theorie“, in der er vier reine Urfarben (Rot, Gelb, Grün, Blau) nennt. Mit der Gegenfarben-Theorie kann unter anderem die Kontrastierung beim Farbensehen erklärt werden (wie z. B. der Simultan- oder Sukzessivkontrast). Die Theorien von Hering und Helmholtz führten lange Zeit zu heftigen Diskussionen, bis man feststellte, dass sowohl die Dreikomponenten-Theorie als auch die Gegenfarben-Theorie ihre Richtigkeit hat, da sich beide auf verschiedene Stufen der Reizverarbeitung im Auge beziehen.
#
Albert Henry Munsell (1858-1918)
Der Maler Albert Munsell entwickelte 1915 ein Farbordnungssystem, das als erstes auf der empfindungsgemäßen Gleichabständigkeit der Farben beruht. Dieses Farbordnungssystem wird auch als Munsell Book of Color bezeichnet und wird heute überwiegend in den USA verwendet. Neben dem Munsell-Farbensystem sind heute noch andere Farbordnungssysteme wie das RAL- oder DIN-Farbkartensystem im Einsatz.
#
Johannes Itten (1888-1967)
Der hauptsächliche Bestandteil des theoretischen Werks von Johannes Itten ist die genaue Festlegung von sechs Grundfarben und das Kontrastverhalten dieser Farben zueinander. So erreichen einzelne Farben erst im Zusammenspiel mit anderen Farben ihren eindeutigen Ausdruck und genauen Sinn. Die sechs Grundfarben teilt er in Farben erster Ordnung (Gelb, Rot und Blau) und Farben zweiter Ordnung (Grün, Orange und Violett) ein, wobei die Farben zweiter Ordnung Mischfarben von Farben der ersten Ordnung sind.
#
Commission Internationale de L’Eclairage (CIE)
Die Internationale Beleuchtungskommission CIE definierte 1931 das so genannte XYZ-Normfarbsystem und den CIE-Normalbeobachter, die heute für die additive Farbmischung weltweite Bedeutung haben. Die CIE wurde 1913 gegründet und ist eine professionelle Organisation, die sich dem Wissensaustausch und der Grundlagenforschung im Bereich der Licht- und Beleuchtungstechnik widmet. Die CIE ist eine Autorität auf diesem Gebiet und wird von der ISO (International Organisation for Standardization, Internationale Normungsorganisation) als Normungsausschuss anerkannt.
#
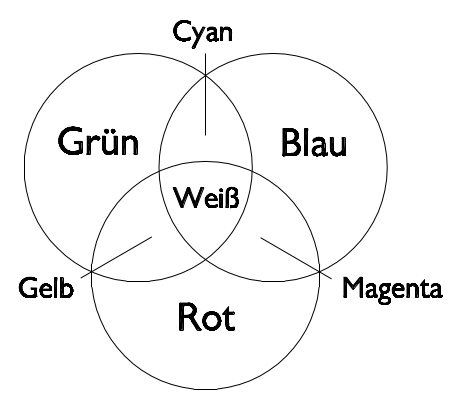
Additive Farbmischung
Beim Zusammenfügen der drei additiven Grundfarben (Primärfarben) Rot, Grün und Blau in gleichen Teilen entsteht die Farben Weiß. Alle anderen Farben ergeben sich aus dem Mischungsverhältnis der drei additiven Grundfarben. Werden nur zwei der drei additiven Grundfarben gemischt, erhält man als Mischfarbe eine subtraktive Grundfarbe, die auch als Komplementärfarbe (Sekundärfarbe) bezeichnet wird. Komplementärfarben sind Farben, die. mit einer Primärfarbe gemischt, weißes Licht ergeben. Als kompensative Farben werden Farben bezeichnet, aus denen man durch additive Mischung eine unbunte Farbe (Schwarz-Grau-Weiß) mischen kann.
Das Prinzip der additiven Farbmischung wird bei selbstleuchtenden Oberflächen (Fernseher, LED-Wände) oder bei der Farbmischung durch Projektion eingesetzt. Die Farbempfindung im Auge geschieht ebenfalls über eine additive Farbmischung.
#
Spektrale Darstellung der additiven Farbmischung:
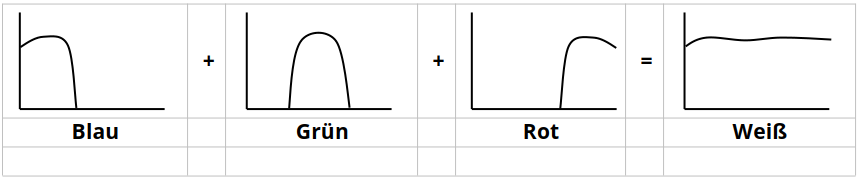
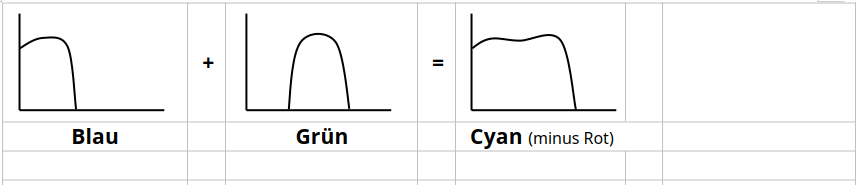
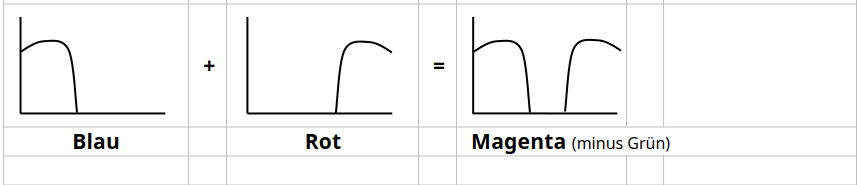

#
RGB-Farbmodell
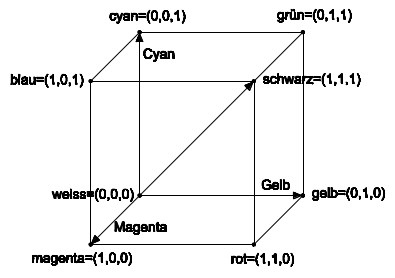
Das RGB-Farbmodell basiert auf dem Prinzip der additiven Farbmischung. Mit den drei additiven Grundfarben (Rot, Grün, Blau) und den drei subtraktiven Grundfarben (Cyan, Magenta, Gelb) sowie Weiß und Schwarz können Farbräume definiert werden, in denen eine bestimmte Farbe anhand von Koordinaten angegeben werden kann. Die drei Grundfarben Rot, Grün und Blau (auch als Primärvalenzen bezeichnet) werden als Farbwerte definiert und mit den Buchstaben RGB abgekürzt. Die Farbe Weiß entsteht aus den RGB-Farbwerten, wenn jeder Farbwert die Größe 1 hat.
Mit den RGB-Farbwerten lässt sich ein dreidimensionaler Farbraum aufspannen, wobei jede Grundfarbe in eine unterschiedliche Richtung zeigt. Die Spitzen der drei Basisvektoren stellen die Farben Rot, Grün und Blau dar, der Koordinatenursprung ist Schwarz.
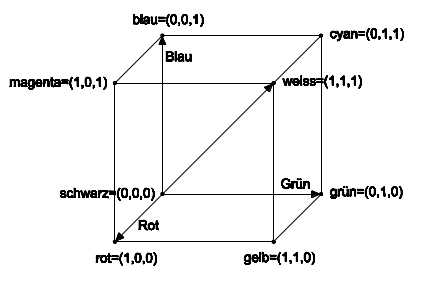
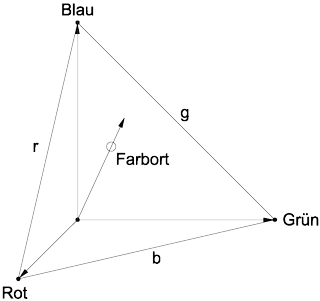
Werden die drei Endpunkte der RGB-Farbwerte miteinander verbunden, entsteht eine dreieckförmige Ebene. Diese Ebene gibt Farborte für beliebige Mischfarben an. Durchstößt der Vektor einer Farbe die Ebene, ausgehend vom Unbuntpunkt (Schwarz), wird der Farbort anhand der Farbwertanteile r,g und b bezeichnet, wobei r + b + g = 1 ist.
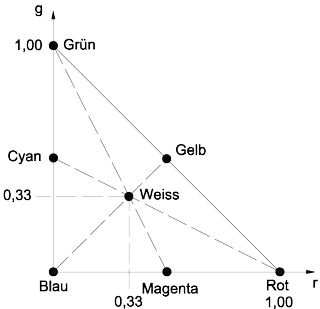
Die Farbwertanteile berechnen sich über eine Transformation der RGB-Farbwerte. Zur Kennzeichnung eines Farbortes sind nur zwei Farbwertanteile ausreichend, der Dritte lässt sich berechnen. Je näher der Farbvektor dem Weißpunkt bei r = g = b = 0,333 kommt, desto entsättigter ist die Farbe. Die Helligkeit einer Farbe kann in diesem System nicht ohne weiteres dargestellt werden, da sie über die Länge des Farbvektors angegeben wird. Das RGB-Farbmodell ist das Standardmodell für Grafik- und Fernsehbildschirme (Selbststrahler).
#
Subtraktive Farbmischung
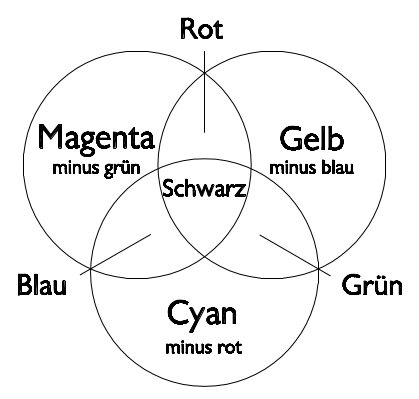
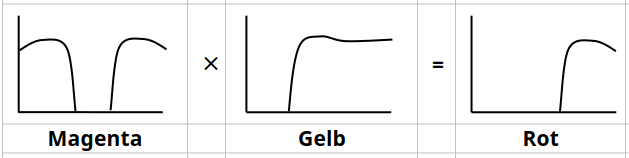
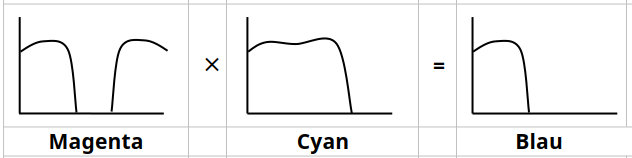
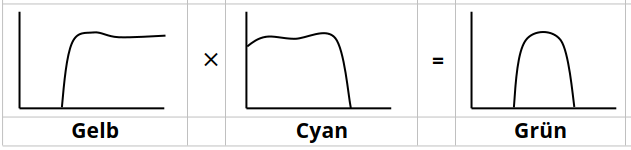
Bei der subtraktiven Farbmischung werden bestimmte Wellenlängen aus dem Lichtspektrum entfernt. Die subtraktiven Grundfarben Cyan, Magenta und Gelb ergeben gemischt Schwarz (alle Wellenlängen sind aus dem Spektrum entfernt). Alle anderen Farben ergeben sich aus dem Mischungsverhältnis der drei subtraktiven Grundfarben. Werden nur zwei der drei Farben gemischt, erhält man als Mischfarbe eine additive Grundfarbe. Dieses Prinzip wird beim Malen, Drucken und bei der Filterung von Licht durch Farbfilter eingesetzt.
Alle Körperfarben entstehen durch subtraktive Farbmischung. Je nach Oberflächen-beschaffenheit bzw. Pigmenteigenschaften eines Körpers werden bestimmte Wellenlängen auftreffender Lichtstrahlen reflektiert oder absorbiert. Das Ergebnis einer subtraktiven Farbmischung hängt nicht alleine von der Farbe der gemischten Farbmittel (wie bei der additiven Farbmischung), sondern auch von deren Eigenschaften ab. Bei Verwendung von Pigmentfarben wirken die einzelnen Farbpartikel wie breitbandige Farbfilter.
#
Spektrale Darstellung der subtraktiven Farbmischung:
Bei der subtraktiven Farbmischung müssen die Transmissionsgrade (von z. B. Farbfiltern) bzw. die Reflexionsgrade (von z. B. Pigmentfarben) miteinander multipliziert werden. Das einfachste Beispiel für die subtraktive Darstellung ist das Hintereinanderschalten mehrerer Farbfilter, wobei die einzelnen Transmissionsgrade miteinander multipliziert werden.
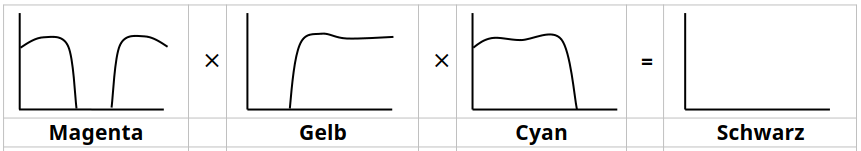
#
CMY-Farbmodell
Das CMY-Farbmodell (Cyan, Magenta, Yellow) benutzt die gleiche Teilmenge des kartesischen Koordinatensystems wie das RGB-Farbmodell. Anstelle von Schwarz im Unbuntpunkt 0,0,0 liegt hier jedoch Weiß im Unbuntpunkt, von dem die drei Farbwerte Cyan, Magenta und Gelb ausgehen. Bei der Angabe einer Mischfarbe wird die subtraktive Farbmischung verwendet, d. h., es wird angegeben, welche Farbe von Weiß entfernt werden muss, um die gewünschte Mischfarbe zu erhalten. Das CMY-Farbmodell wird in der Druckindustrie angewendet, in der mit Körperfarben (Farbpigmente auf einem Untergrund) gearbeitet wird. Ein erweitertes Farbmodell mit der Bezeichnung CMYK benutzt als vierte Farbe Schwarz (K für black). Ausgehend vom CMY-Farbmodell wird hier Schwarz anstelle gleicher Anteile von Cyan, Magenta und Yellow verwendet. Mit einfachen Transformationen können die acht möglichen RGB-Farben einer Bildschirmanzeige in die acht möglichen CMY-Farben einer Druckausgabe umgewandelt werden. Dies ist besonders wichtig für den Druck einer Bildschirmansicht.
#
Integrierte Farbmischung
Der Grafiker Harald Küppers entdeckte und formulierte das Gesetz der integrierten Farbmischung, das sich auf die Mischung deckender Farbmittel (Farbpigmente) bezieht und besonders wichtig im Bereich der Druckindustrie ist. Bei der integrativen Farbmischung entsteht die Farbenvielfalt nicht durch das Zusammenwirken von 3 Grundfarben wie bei der additiven oder subtraktiven Farbmischung. Stattdessen müssen bei der integrativen Farbmischung 8 Grundfarben als deckende Farbmittel zur Verfügung stehen. Diese Grundfarben sind Weiß, Schwarz, Gelb, Rot, Magenta, Blau, Cyan und Grün. Ausgenommen die Unbuntfarben Schwarz und Weiß ergeben die Grundfarben einen Farbkreis, der in dieser Reihenfolge auch in anderen Farbmodellen verwendet wird und in ähnlicher Form schon von Goethe definiert wurde.
Bei der integrativen Farbmischung herrscht das Prinzip des Mengenaustausches. Es wird immer von einer deckenden Farbschicht ausgegangen, die entsprechende Mengenanteile der Grundfarben enthält, unabhängig von einer Farbnuance. Die deckende Farbschicht kann jedoch nur aus maximal 4 Teilmengen (Grundfarben) zusammengemischt sein. Grundsätzlich besteht jede Farbnuance aus einer Unbuntmenge und einer Buntmenge. Die Unbuntmenge wird ausschließlich über die beiden unbunten Grundfarben Weiß und Schwarz gebildet, und die Buntmenge aus zwei (im Farbenkreis) benachbarten Grundfarben. Aus dieser Konstellation können sich nur sechs Gruppen der Grundfarben bilden, wobei jede Gruppe die Unbuntfarben Weiß und Schwarz beinhaltet. Die einzelnen bunten Gruppen sind Gelb-Rot, Rot-Magenta, Magenta-Blau, Blau-Cyan, Cyan-Grün und Grün-Gelb. Über die bunten Gruppen lassen sich alle Farbnuancen erzeugen, die mit den Unbuntfarben Weiß und Schwarz für eine Entsättigung oder Verdunkelung ausgemischt werden können. Dieses Prinzip der Unbunt-Ausmischung ist sehr ökonomisch, da keine bunten Farben für die Erzeugung einer unbunten Farbe verwendet werden (wie bei der kompensativen Farbmischung). Zusätzlich führt es zu einer größeren Sicherheit bei der Herstellung einer gewünschten Mischfarbe.
#
HSV(HSB)-Farbmodell
Im Gegensatz zu den hardwareorientierten RGB/CMY-Farbmodellen richtet sich das HSV-Farbmodell an der menschlichen Empfindung aus. HSV steht dabei für Hue (Farbton), Saturation (Sättigung) und Value (Helligkeitswert). In einigen Fällen wird der Value-Parameter durch die Brightness (B) ersetzt. Das HSV-Farbmodell basiert auf den intuitiven Mischungsmethoden eines Malers und verwendet eine sechsseitige Pyramide in einem zylindrischen Koordinatensystem zur Darstellung des Farbenraums. Die Helligkeits-Ebene bei V=1 entspricht einer Ebene, in der alle RGB-Werte gleich 1 sind. Die Helligkeits-Ebene ist eine Projektion entlang der Hauptdiagonalen von Schwarz nach Weiß im RGB-Farbmodell.
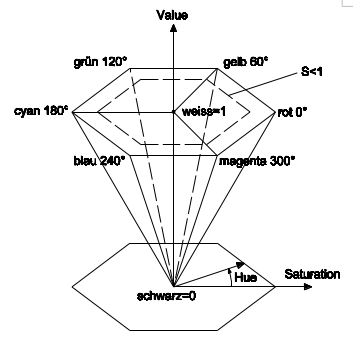
Der Farbton H wird über den Winkel um die vertikale Helligkeitsachse V festgelegt. Die Komplementärfarben liegen im HSV-Farbmodell um 180° zueinander versetzt. Die Sättigung S eines Farbtons liegt zwischen 0 an der vertikalen Achse und 1 an den Seiten der Pyramidenoberfläche. Hierbei muss beachtet werden, dass die Sättigung nicht gleichzusetzen ist mit dem Abstand von der vertikalen Helligkeitsachse. Eine Sättigung von 1 hat bei einer Helligkeit von 0,5 einen anderen Abstand zur Mittelachse als bei einer Helligkeit von 1. Sättigungen kleiner 1 liegen immer auf einer parallelen Linie zu den Pyramidenkanten. Um den Wert der Sättigung gleichzusetzen mit dem Abstand von der Mittelachse wird der Farbkörper des HSV-Modells auch öfter als Zylinder dargestellt. Im HSV-Farbmodell ist eine Sättigung, die größer ist als die Helligkeit, nicht zulässig (S≤V).
Die vertikale Achse der Helligkeitswerte (V) bezeichnet alle unbunten Farben, beginnend bei Schwarz (0) über Grau nach Weiß (1). Die unbunten Farben enthalten keine Sättigung (S = 0). Ist die Sättigung größer null, entsteht eine Mischfarbe aus einer unbunten Farbe und einer bunten Farbe. Jede Farbe bei V = 1 und S = 1 entspricht den reinen Pigmenten eines Malers, die als Ausgangspunkt beim Mischen von Farben dienen. Einer Änderung des Farbtons H entspricht die Wahl der reinen Pigmente für die Farbmischung. Das Hinzufügen von weißen Pigmenten bewirkt eine Verminderung der Sättigung (S) ohne Änderung der Helligkeit (Tint, Auftönen). Shades (Abtönen) entstehen, wenn die Sättigung beibehalten, aber die Helligkeit (V) vermindert wird (bzw. Schwarz hinzugefügt). Tones entstehen bei der Verminderung der Sättigung (S) und der Helligkeit (V) bzw. dem Hinzufügen schwarzer und weißer Pigmente zu einem reinen Pigment.
#
HLS-Farbmodell
Das HLS-Farbmodell wurde von der Firma Tektronix entwickelt und baut auf das HSV-Farbmodell auf. Es besteht im Gegensatz zum HSV-Farbmodell aus einer sechsseitigen Doppelpyramide. Die Grundprinzipien sind dabei ähnlich dem HSV-Farbmodell und basieren auf den Mischungsmethoden eines Malers. HLS steht für Hue (Farbton), Lightness (Helligkeit) und Saturation (Sättigung).
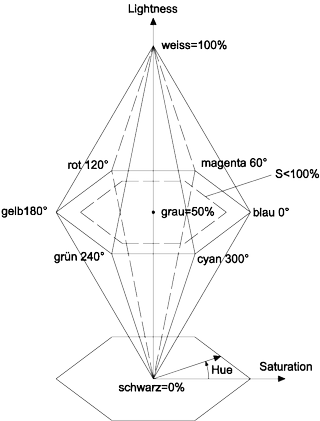
Die Helligkeit L und die Sättigung S werden in Prozentwerten angegeben. Die Helligkeit V des HSV-Farbmodells wird hier durch die Lightness L ersetzt, die bei R = G = B = 1 einen Wert von L = 50 % hat. Die Berechnung von H entspricht der des HSV-Raumes, jedoch mit dem Unterschied, dass die Farben um 120° gegen den Uhrzeigersinn gedreht sind, so dass die Farbe Blau bei H = 0° liegt. Viele Programme der Computergrafik benutzen aber mittlerweile beim HLS-Farbmodell die gleichen Farbwinkelangaben wie das HSV-Farbmodell.
Im Gegensatz zum HSV-Farbmodell hat die Sättigung im HLS-Farbmodell eine unterschiedliche Bedeutung. Während man im HSV-Farbmodell eine Farbe mit RGB > 0 als nicht voll gesättigt betrachtet, ist dies im HLS-Farbmodell möglich. Dies trifft zu für alle Farben auf den Außenflächen der Doppelpyramide, ausgenommen die Farben der Ebene bei L = 50 %. Diese Farben entsprechen alle denen der Helligkeitsebene mit V = 1 des HSV-Farbmodells, ausgenommen Weiß, das im HLS-Farbmodell ein Grauton ist.
#
Dreifarbentheorie
Aufgrund empirischer Experimente wurde festgestellt, dass alle in der Natur vorkommenden Farben durch eine Addition der drei Grundfarben (Primärfarben) Rot, Grün und Blau hergestellt werden können. Für die Auswahl der drei Primärfarben (Farbtripel) gilt, dass keine der Primärfarben durch eine Kombination der beiden anderen Primärfarben erzeugt werden kann.
Aus den theoretisch unendlich vielen Primärfarben hat 1931 die Internationale Beleuchtungs-kommission (CIE) für Untersuchungen folgende Primärfarben festgelegt, die auch Primärvalenzen genannt werden:
Rot (R) = 700,00 nm
Grün (G) = 546,10 nm
Blau (B) = 435,80 nm
Die Wahl dieser Primärvalenzen ist prinzipiell willkürlich und alleine durch technische Begebenheiten bestimmt. So sind die Wellenlängen für Gelb und Blau typische Spektrallinien aus dem Quecksilberspektrum.
Um quantitative Aussagen über die Farbmischung treffen zu können, wurden in umfangreichen Experimenten mit Testpersonen vorgegebene Farben durch Anteile der drei festgelegten Primärvalenzen (RGB) über eine additive Farbmischung nachgebildet.
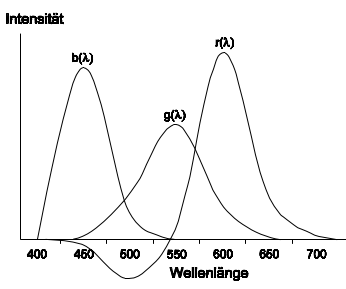
Dabei werden die in das Auge des Beobachters einfallenden Lichtstrahlen als Farbreize wahrgenommen, die über drei voneinander unabhängige Spektralwertfunktionen (Augenempfindlichkeitsfunktionen) ausgedrückt werden können.
Das Ergebnis der Farbmischexperimente sind die CIE-Farbmischkurven; Sie definieren einen farbmetrischen Beobachter. Hierbei fällt auf, dass die rote Spektralwertfunktion zum Teil negative Werte besitzt. Dies liegt daran, dass die Sättigung einer Mischfarbe bei additiver Mischung nicht größer sein kann als die Sättigung der Grundfarbe. Aus diesem Grund muss mit den gewählten Primärvalenzen theoretisch ein Teil der roten Farbe im Bereich von 445 nm bis 550 nm subtrahiert werden, um eine entsprechende Sättigung der Mischfarbe zu erreichen. Es können somit nicht alle vom Auge wahrnehmbaren Farben durch direkte additive Mischung der drei festgelegten Primärvalenzen RGB erzeugt werden.
#
CIE-Normfarbwerte (XYZ-Farbsystem)
Die CIE-Farbmischkurven sind wegen des negativen Rotanteils nicht für eine praktische Anwendung geeignet. Um diesen Nachteil auszugleichen, hat die CIE neue Primärvalenzen festgelegt, deren Spektralwertfunktionen nur noch positive Werte besitzen und mit denen alle vom Auge wahrnehmbaren Farben durch eine direkte Mischung erzielt werden können.
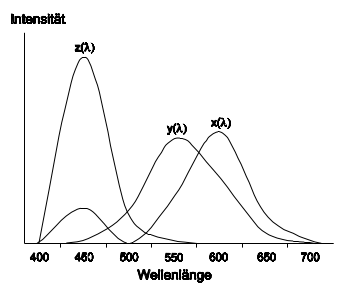
Diese neuen Primärvalenzen sind jedoch physikalisch nicht mehr darstellbar, d.h., man kann sie nicht aus dem Sonnenlicht herausfiltern, weil deren Farbsättigung teilweise größer als 100 % ist. Aus diesem Grund werden die neuen Primärvalenzen als X(Rot), Y(Grün), Z(Blau) bezeichnet und virtuelle Primärvalenzen (virtuelle Tristimulus-Werte) oder auch Normfarbwerte genannt. Die virtuellen Primärvalenzen XYZ sind durch eine lineare Transformation mit den reellen Primärvalenzen RGB verknüpft.
Da die virtuellen Primärvalenzen im Spektrum des Sonnenlichts nicht vorkommen, können deren Spektralwertkurven nicht die spektrale Verteilung der virtuellen Primärvalenzen wiedergeben. Die Spektralwertkurven sind lediglich Hilfsfunktionen, mit denen man berechnen kann, in welchen Anteilen man die virtuellen Primärvalenzen XYZ mischen muss, um eine beliebige Farbe des Sonnenlichts zu erhalten.
Bei der Wahl der virtuellen Primärvalenzen wurde bewusst eine Spektralwertfunktion y(λ) gewählt, die identisch mit der spektralen Helligkeitsempfindungskurve V(λ) ist. Somit enthält der Normfarbwert Y die Helligkeitsinformation, X korrespondiert mit dem Rot-Grün-Anteil und Z mit dem Blau-Gelb-Anteil einer Farbe.
Jeder Beobachter (sprich Mensch) hat drei ihm eigentümliche Spektralwertfunktionen, die für die meisten farbnormalsichtigen Menschen annähernd gleich sind. Für die Farbbewertung in der Technik benutzt man die von der CIE festgelegten Spektralwertfunktionen der drei virtuellen Primärvalenzen. Diese Spektralwertfunktionen wurden aus einer ausreichenden Anzahl individueller Beobachter (Normalbeobachter) ermittelt und werden auch als Normspektralwertfunktionen bezeichnet.
#
CIE-Normalbeobachter
Die drei Spektralwertfunktionen (und damit die Farbvalenzen) hängen wesentlich von der Gesichtsfeldgröße des Beobachters ab. Aus diesem Grund wurden von der CIE verschiedene Gesichtsfeldgrößen definiert.
#
2°-Normalbeobachter
Der 2°-Normalbeobachter dient der Bestimmung der Farbvalenz für eine Gesichtsfeldgröße, die gleich oder kleiner 4° ist. Dieses Gesichtsfeld entspricht einem Objekt mit einem Durchmesser von 1,75 cm bei einem Betrachtungsabstand von 50 cm und wird als „farbmetrischer 2°(Kleinfeld)-Normalbeobachter CIE 1931“ bezeichnet.
#
10°-Normalbeobachter
Der 10°-Normalbeobachter wurde zusätzlich von der CIE 1964 empfohlen. Er dient der Bestimmung der Farbvalenz für eine Gesichtsfeldgröße über 4°. Dieses Gesichtsfeld entspricht einem Objekt mit einem Durchmesser von 8,75 cm bei einem Betrachtungsabstand von 50 cm und wird als „farbmetrischer 10°-Normalbeobachter CIE 1964“ bezeichnet. Eine Umrechnung auf das 2° System ist grundsätzlich nicht möglich, da man leicht abweichende Spektralwertfunktionen mit zum Teil merklichen Farbortverschiebungen der Wellenlängen erhält.
Die CIE-Normalbeobachter sind in der DIN 5033, Teil 2, näher spezifiziert.
Mit Hilfe dieser genauen Spezifizierung lassen sich Farbsysteme entwickeln, mit denen Farben eindeutig nach ihrer Farbart eingeordnet werden können.
#
CIE-Normfarbtafel
Die Normfarbwerte XYZ liefern Informationen über Helligkeit, Farbton und Sättigung einer Farbe. Da die Normfarbwerte nicht ohne weiteres visuell anschaulich sind, werden die Normfarbwerte XYZ mittels einer Transformation in die Normfarbwertanteile xyz (nicht zu verwechseln mit x(λ), y(λ) und z(λ)) überführt.
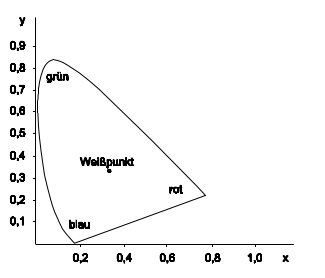
Der Normfarbwertanteil z kann aus x und y ermittelt werden, da x + y + z = 1 ist. Werden die Normfarb-wertanteile x und y für alle Wellenlängen ermittelt, entsteht ein nicht geschlossener Spektralfarbenzug (siehe Bild 5.11), der auch als Planck’scher Kurvenzug bezeichnet wird. Die Verbindungsgerade zwischen den Endpunkten des Spektralfarbenzugs heißt Purpurgerade.
Die so umschlossene Fläche ist eine Darstellung der empfindungsgemäßen Menge aller vom Menschen wahrnehmbaren Farben. Unterschieden wird dabei zwischen der Normfarbtafel für den 2°-Normbeobachter und den 10°-Normbeobachter, wobei zwischen beiden leichte Flächendifferenzen vorkommen.
Mit den x- und y-Koordinaten können einzelne Farben präzise beschrieben werden, wobei mit x und y nur der Farbton und die Sättigung angeben wird. Die Helligkeit der Farbe muss separat mit dem Normfarbwert Y definiert werden (nach der V(λ)-Kurve). Eine Änderung der Helligkeit bedeutet eine Verschiebung der Normfarbtafel auf der z-Achse des Koordinatensystems. Jede Farbe besitzt nur einen Farbort in der Normfarbtafel.
Etwa in der Mitte der Normfarbtafel liegt der Weißpunkt (Unbuntpunkt) mit den Koordinaten x = y = z = 0,33 (x=0,33, y=0,33). Hier sind alle Farben vollkommen entsättigt. Dieser Punkt wird auch als Gleichenergie-Weiß oder Referenz-Weiß bezeichnet. Die (unbunte) Farbe Schwarz lässt sich nicht darstellen, da für Schwarz x+y+z=1 gilt.
Am Rand des Planck’schen Kurvenzugs liegen alle im Spektrum vorkommenden Spektralfarben. Im Gegensatz dazu kommen die Farben auf der Purpurgeraden nicht als Wellenlängen im sichtbaren Spektrum vor. An der Purpurlinie liegen additive Mischfarben aus Blau und Rot, die vom Auge als Farbe (Purpur bzw. Magenta) wahrgenommen werden. Die linke untere Ecke der CIE-Normfarbtafel entspricht dem kurzwelligen Ende des sichtbaren Spektrums mit 380 nm (Blau). Der obere Scheitel stellt die Wellenlänge 520 nm (Grün) dar und die rechte äußere Ecke entspricht dem langwelligen Ende des Spektrums mit 780 nm (Rot).
Zieht man eine Gerade vom Weißpunkt zu einzelnen Spektralfarben des Kurvenzugs, erhält man die Gerade der farbtongleichen Farben, d.h., die Sättigung der Farbe nimmt zum Rand des Spektralfarbenzugs zu und beträgt auf dem Spektralfarbenzug 100 %. Werden in der CIE-Normfarbtafel zwei beliebige Farben mit einer Geraden verbunden, liegen auf der Geraden alle Farben, die durch eine additive Farbmischung der beiden Ausgangsfarben mit verschiedenen Sättigungen erreicht werden können. Gegenüberliegende Farben auf der Geraden werden dabei als Komplementärfarben bezeichnet und ergeben nach einer additiven Farbmischung Weiß. Farben, aus denen man mit einer additiven Farbmischung eine unbunte Farbe (z. B. Hellgrau) mischen kann, werden als kompensative Farben bezeichnet.
#
Color Gamut
Mit Hilfe der CIE-Normfarbtafel ist es möglich, eine Farbpalette zu definieren, die das Ergebnis der Addition von beliebigen Farben zeigt (Gamut). Auf diese Weise werden zum Beispiel Farbpaletten für das Farbfernsehen, Film oder Druck darstellbar und miteinander vergleichbar. Werden die Farborte von drei beliebigen Farben A, B und C in der CIE-Normfarbtafel untereinander verbunden, entsteht eine dreieckige Fläche. Alle in dieser Fläche enthaltenen Farben lassen sich aus einer additiven Mischung der Farben A, B, und C erzeugen.
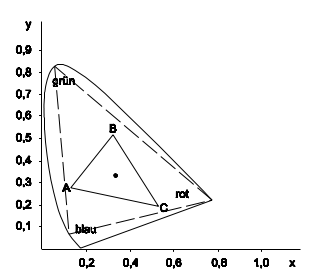
Die dreieckige Fläche erklärt zudem, warum sich aus den von der CIE 1931 festgelegten Primärvalenzen (siehe Kapitel 5.12: Dreifarbentheorie) nicht alle sichtbaren Farben erzeugen lassen. Selbst wenn die gewählten Primärvalenzen auf dem Spektralfarbenzug liegen, lassen sich mit dem entstehenden Dreieck nicht alle Farben der CIE-Normfarbtafel abdecken (siehe gestrichelte Linie in Bild 5.12).
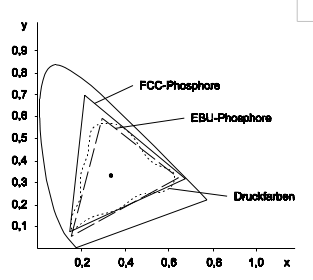
n der CIE-Normfarbtafel lassen sich so Farbpaletten verschiedener Farbsysteme eintragen und miteinander vergleichen. In Bild 5.13 sind die Gamut-Paletten für Druckfarben und die Phosphore des Farbfernsehens eingetragen (EBU = PAL-Farbfernsehsystem für Deutschland, FCC = NTSC-Farbfernsehsystem für die USA). So werden sehr schnell die Farbspektren der verschiedenen Systeme deutlich und vergleichbar. Da die Gamut-Palette für Druckfarben gegenüber den Fernseh- und Monitorphosphoren relativ klein ist, muss für einen farbechten Ausdruck von Monitorbildern die Farbpalette des Monitors reduziert werden. Andernfalls ist eine exakte Reproduktion nicht möglich.
#
CIE-Farbabstandsräume
Die in der CIE-Normfarbtafel definierten trichromatischen Farbmaßzahlen sind nicht zur empfindungsgemäßen Bewertung von Farben geeignet. In der CIE-Normfarbtafel werden Farben in gleicher Entfernung vom Unbuntpunkt als nicht gleich gesättigt empfunden.
Ebenfalls drücken sich empfindungsgemäße Unterschiede hinsichtlich des Farbtons nicht in einer proportionalen Differenz der Wellenlänge aus. Die trichromatischen Farbmaßzahlen sind nur in der Lage, Farbreize eindeutig zu kennzeichnen. Dies liegt daran, dass sie lediglich auf den Gesetzmäßigkeiten der additiven Farbmischung beruhen, keinen Bezug nehmen auf die Physiologie des Farbensehens und in einem Raum dargestellt werden, in dem keine Abstandsbegriffe für Farben existieren.
Die Basis einer empfindungsgemäßen Farbabstands-bewertung ist die Messung von Farbunterschiedsschwellen. Man spricht von einem wahrnehmbaren Farbunterschied, wenn sich zwei vorgegebene Farben gerade farblich unterscheiden, der sog. Farbabstandsschwelle. Diese Farbabstandsschwellen werden in der CIE-Normfarbtafel über die MacAdam-Ellipsen sichtbar. In der CIE-Normfarbtafel liegen die Farborte für die Schwellenabstände auf Ellipsen, deren Radien und Richtungen vom Farbort der Normfarbtafel abhängen. Innerhalb der MacAdam-Ellipsen liegen Farben, die vom Auge als eine einzige Farbe wahrgenommen werden. Die MacAdam-Ellipsen zeigen somit sehr deutlich die empfindungsgemäße Inhomogenität der CIE-Normfarbtafel.
.png)
In der industriellen Farbmetrik ist es jedoch äußerst wichtig, Farbunterschiede möglichst empfindungsgemäß zu quantifizieren. Aus diesem Grund wurden von der CIE weitere Farbtafeln definiert, um die Forderung der empfindungsgemäßen Darstellung zu erfüllen. Zu diesen Systemen gehören die CIE-UCS-, CIE-LUV- und CIE-LAB-Normfarbtafeln, die 1976 von der CIE spezifiziert wurden.
Die CIE-Normfarbtafeln sind in der DIN 5033, Teil 3, näher erläutert.
#
CIE-UCS-Farbtafel
Die CIE-UCS-Farbtafel (Uniform Chromity Scale) ist ein Kompromiss zur empfindungsgemäßen Darstellung von Farben. Die CIE-UCS-Farbtafel besteht aus den Koordinaten u und v, bzw. u’ und v’, die sich aus den x- und y-Koordinaten der CIE-Normfarbtafel über eine Transformation berechnen. Die Transformation für die u- und v- Koordinaten wurde von der CIE 1960 vorgeschlagen und 1976 durch eine verbesserte Transformation mit den u’- und v’- Koordinaten ersetzt. Die CIE-UCS-Farbtafel wird auch als uv-Farbtafel bzw. u’v’-Farbtafel bezeichnet. Diese Farbtafel kommt einer empfindungsgemäßen gleichabständigen Farbtafel näher als die CIE-Normfarbtafel, wie in Bild 5.15 anhand der MacAdam-Ellipsen zu sehen. Für die Darstellung abbildbarer Farbräume oder die Darstellung selbstleuchtender oder fluoreszierender Farben wie z. B. bei farbigen Bildschirmen ist die u’v’-Farbtafel allen anderen Darstellungen deutlich überlegen. Wie bei der CIE-Normfarbtafel liegen alle Mischfarben zweier beliebiger Farben auf einer Geraden zwischen den beiden Farben. In der CIE-UCS-Farbtafel lassen sich jedoch nur Unterschiede gleichheller Farben beurteilen.
.png)
#
CIE-LUV-System
1976 wurde von der CIE das dreidimensionale CIE-LUV-System zur Farbbeschreibung vorgestellt, um auch Unterschiede ungleich heller Farben zu beurteilen. Das CIE-LUV-System basiert auf der CIE-UCS-Farbtafel und gibt Farbdifferenzen annähernd empfindungsgemäß wieder. Die Koordinaten u’ und v’ werden unter Berücksichtigung des Normfarbwerts Y (Helligkeit) in helligkeitsbezogene Koordinaten mit der Bezeichnung u* und v* umgerechnet. Zur vollständigen Beschreibung wird die empfindungsgemäße Helligkeitsfunktion mit der Bezeichnung L* (Luminanz) aus dem Normfarbwert Y berechnet.
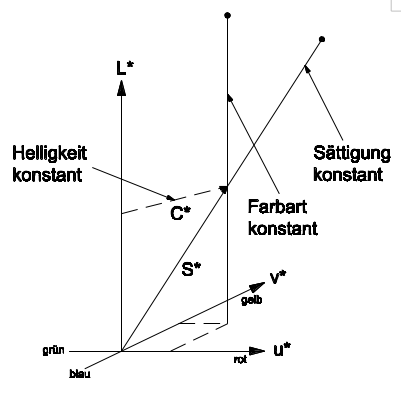
Die Luv-Maßzahlen werden in ein dreidimensionales Koordinatensystem ein-getragen, wobei der Schnittpunkt der drei Achsen der Unbuntpunkt Schwarz darstellt (L = 0, u* = 0, v* = 0). Die vertikalen Helligkeitsachse L* ist die Unbuntgerade und gibt die Helligkeit einer Farbe an (L* > 0). Die u-Achse verläuft in Rot-Grün-Richtung (u > 0 = Rot, u* < 0 = Grün), die v-Achse in Gelb-Blau-Richtung (v > 0 = Gelb, v* < 0 = Blau). Aus den beiden Koordinaten u* und v* lässt sich qualitativ ein Farbton ableiten.
Im Rahmen des CIE-LUV-Koordinatensytems ist die zahlenmäßige Kennzeichnung einer Farbe nach Helligkeit, Farbton und Sättigung möglich. Bei Angaben dieser Größen ist immer der Zusatz „CIE-LUV-1976“ erforderlich, um die Größen eindeutig zu kennzeichnen. Diese Maßzahlen sind besonders für das grafische Gewerbe interessant, da hiermit Farbunterschiede objektiv (empfindungsgemäß) spezifiziert werden können.
Die psychometrische Buntheit C* (hier nicht zu verwechseln mit der Sättigung) gibt den horizontalen Abstand einer Farbe von der Unbuntgeraden an. Bei Veränderung der Helligkeit L* verändert sich der Abstand des Farborts zur Unbuntgeraden nicht. Es ändert sich lediglich die Farbart (Farbton und Sättigung). Die psychometrische Sättigung S* stellt die diagonale Entfernung des jeweiligen Farborts zum Unbuntpunkt in der Farbtafel dar. Der Farbton lässt sich durch einen Farbtonwinkel angeben.
Das CIE-LUV-System ist kein Primärvalenzsystem, da Luv* nur Farbkoordinaten und keine Farbwerte angibt. Farben gleicher Farbart (Farbton und Sättigung) liegen in diesem System ebenfalls auf einer Geraden durch den Koordinatenursprung, allerdings liegen verschiedene additive Mischungen zweier Farben im CIE-LUV-Farbraum nicht auf einer Geraden zwischen den Farben.
Das CIE-LUV-System wird heute vorwiegend für die Farbbestimmung von Selbstleuchtern (wie z. B. Farbfernsehgeräten) angewendet.
#
CIE-LAB-System
Da die empfindungsgemäße Gleichabständigkeit der Farben im CIE-LUV-System keineswegs vollkommen ist, hat die CIE 1976 das „CIE-LAB-1976“-Farbkoordinatensystem definiert, das ebenfalls in der DIN 6174 verankert ist. Im CIE-LAB-System wird ein standardisierter und idealisierter Farbraum dargestellt, in dem alle vom Menschen wahrnehmbaren Farben annähernd empfindungsgemäß repräsentiert werden. Dieses System ist eine Weiterentwicklung des CIE-LUV-Systems und arbeitet mit den Koordinaten Lab*.
Die Helligkeitsfunktion L* des CIE-LAB-Systems ist identisch mit der des CIE-LUV-Systems. Die Achsen a* und b* sind die Buntheitsachsen für Rot-Grün (a*) und Blau-Gelb (b*). Im Schnittpunkt der ab-Achsen verläuft die Unbuntgerade von L* = 0 für Schwarz bis L* = 100 für Weiß.
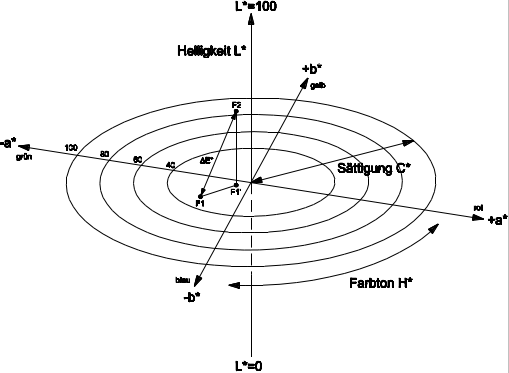
Auch im CIE-LAB-Koordinatensytem ist die zahlenmäßige Kennzeichnung einer Farbe nach Helligkeit (L*) und Farbton (a*, b*) möglich. Aus den ab-Werten lässt sich die Sättigung C* (Chroma, Entfernung vom Unbuntpunkt) und der Farbton H* (Hue, Richtungswinkel vom Unbuntpunkt) ableiten. Bei Angabe dieser Größen ist immer der Zusatz „CIE-LAB-1976“ erforderlich, um die Größen eindeutig zu kennzeichnen.
Das CIE-LAB-System wird in den Anwendungsbereichen bevorzugt, bei denen Körperfarben (von einem Körper reflektiertes Licht einer Lichtquelle) gemessen werden. Die ab-Werte entstehen durch eine Transformation der Normfarbwerte XYZ (virtuelle Primärvalenzen), die in Bezug zu einer unbunten Referenzfarbe (Weiß) stehen. Liegt die Farbart der Lichtquelle weit außerhalb der natürlichen Farbarten wie Tageslicht oder Kunstlicht, können Körperfarben mit diesem Modell nur sehr schlecht beschrieben werden. Je näher die Farbart der Lichtquelle der Judd’schen Geraden in der CIE-Normfarbtafel kommt, desto besser lassen sich Körperfarben mit dem CIE-LAB-System quantifizieren.
Da die geometrischen Farbabstände im Farbraum des CIE-LAB-Systems direkt proportional zu den empfindungsgemäßen Farbabständen sind, können die Farbabstände als zahlenmäßige Werte berechnet werden. Der Farbabstand wird mit E* bezeichnet und ist der direkte Anstand zweier Farben im Farbraum. Bei einem Farbabstand ab ΔE* = 0,5 wird ein gerade noch wahrnehmbarer Farbunterschied bemerkt (siehe Tabelle). In der DIN 53218 wird eine Bewertungsskala mit 6 Stufen für die Beurteilung von Farbunterschieden empfohlen, die jedoch nicht an ein bestimmtes Farbabstandsverfahren gebunden ist.
Auch im CIE-LAB-Koordinatensytem ist die zahlenmäßige Kennzeichnung einer Farbe nach Helligkeit (L*) und Farbton (a*, b*) möglich. Aus den ab-Werten lässt sich die Sättigung C* (Chroma, Entfernung vom Unbuntpunkt) und der Farbton H* (Hue, Richtungswinkel vom Unbuntpunkt) ableiten. Bei Angabe dieser Größen ist immer der Zusatz „CIE-LAB-1976“ erforderlich, um die Größen eindeutig zu kennzeichnen.
Das CIE-LAB-System wird in den Anwendungsbereichen bevorzugt, bei denen Körperfarben (von einem Körper reflektiertes Licht einer Lichtquelle) gemessen werden. Die ab-Werte entstehen durch eine Transformation der Normfarbwerte XYZ (virtuelle Primärvalenzen), die in Bezug zu einer unbunten Referenzfarbe (Weiß) stehen. Liegt die Farbart der Lichtquelle weit außerhalb der natürlichen Farbarten wie Tageslicht oder Kunstlicht, können Körperfarben mit diesem Modell nur sehr schlecht beschrieben werden. Je näher die Farbart der Lichtquelle der Judd’schen Geraden in der CIE-Normfarbtafel kommt, desto besser lassen sich Körperfarben mit dem CIE-LAB-System quantifizieren.
Da die geometrischen Farbabstände im Farbraum des CIE-LAB-Systems direkt proportional zu den empfindungsgemäßen Farbabständen sind, können die Farbabstände als zahlenmäßige Werte berechnet werden. Der Farbabstand wird mit E* bezeichnet und ist der direkte Anstand zweier Farben im Farbraum. Bei einem Farbabstand ab E* = 0,5 wird ein gerade noch wahrnehmbarer Farbunterschied bemerkt (siehe Tabelle). In der DIN 53218 wird eine Bewertungsskala mit 6 Stufen für die Beurteilung von Farbunterschieden empfohlen, die jedoch nicht an ein bestimmtes Farbabstandsverfahren gebunden ist.
| Differenz ΔE* | Bewertung des Farbunterschiedes | nach DIN 53218 | |
|---|---|---|---|
| Stufe | Bewertung | ||
| bis 0,2 | nicht wahrnehmbar | 0 | kein Farbunterschied |
| 0,2 bis 0,5 | sehr gering | 1 | Spur eines Farbunterschieds |
| 0,5 bis 1,5 | gering | 2 | kleiner Farbunterschied |
| 1,5 bis 3,0 | deutlich | 3 | mittlerer Farbunterschied |
| 3,0 bis 6,0 | sehr deutlich | 4 | großer Farbunterschied |
| 6,0 bis 12,0 | stark | 5 | sehr großer Farbunterschied |
| über 12,0 | sehr stark | ||